题目内容
如图,函数f(x)=Asin(ωx+?)(A>0,ω>0,|?|<
)的图象经过点(0,1)

(1)求函数f(x)的解析式;
(2)写出函数f(x)的单调递增区间;
(3)若f(x)=
,求自变量x的值.
| π |
| 2 |

(1)求函数f(x)的解析式;
(2)写出函数f(x)的单调递增区间;
(3)若f(x)=
| 2 |
分析:(1)由函数图象的顶点纵坐标可得A;再由函数的周期求得ω;再由函数的图象过点(0,1),结合|?|<
,求得 ?,从而求得函数的解析式.
(2)令2kπ-
≤
x+
≤2kπ+
,k∈z,求得x的范围,故函数的增区间.
(3)由f(x)=
,求得sin(
x+
)=
,可得
x+
=2kπ+
,或
x+
=2kπ+
,k∈z,由此求得x的值.
| π |
| 2 |
(2)令2kπ-
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
(3)由f(x)=
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 3π |
| 4 |
解答:解:(1)由函数图象的顶点纵坐标可得A=2,再由函数的周期为2[(x0+2π)-x0]=
,求得ω=
.
再由函数的图象过点(0,1),可得2sin?=1,故sin?=
.再由|?|<
,可得 ?=
,
故函数的解析式为 f(x)=2sin(
x+
).
(2)令2kπ-
≤
x+
≤2kπ+
,k∈z,求得 4kπ-
≤x≤4kπ+
,故函数的增区间为[4kπ-
,4kπ+
],k∈z.
(3)若f(x)=
,则有2sin(
x+
)=
,sin(
x+
)=
,∴
x+
=2kπ+
,或
x+
=2kπ+
,k∈z.
解得 x=4kπ+
,或 x=4kπ+
,k∈z.
| 2π |
| ω |
| 1 |
| 2 |
再由函数的图象过点(0,1),可得2sin?=1,故sin?=
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
故函数的解析式为 f(x)=2sin(
| 1 |
| 2 |
| π |
| 6 |
(2)令2kπ-
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 4π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
| 2π |
| 3 |
(3)若f(x)=
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 3π |
| 4 |
解得 x=4kπ+
| π |
| 6 |
| 7π |
| 6 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,复合三角函数的单调性,属于中档题.

练习册系列答案
相关题目
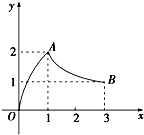
如图,函数f(x)的图象是曲线OAB,则f(
)的值等于( )
| 1 |
| f(3) |

| A、1 | B、2 | C、3 | D、0 |
 如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是( )
如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是( ) 已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象
已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象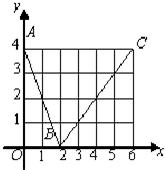 如图,函数f(x)的图象是折线段ABC,其中点A、B、C的坐标分别为(0,4),(2,0),(6,4),若f(x)的值域为[0,4],定义域为[m,n],则|m-n|的最小值为
如图,函数f(x)的图象是折线段ABC,其中点A、B、C的坐标分别为(0,4),(2,0),(6,4),若f(x)的值域为[0,4],定义域为[m,n],则|m-n|的最小值为