题目内容
(2013•浙江模拟)已知直角梯形ABCD中,AD⊥DC,AD⊥AB,△CDE是边长为2的等边三角形,AB=5.沿CE将△BCE折起,使B至B′处,且B′C⊥DE;然后再将△ADE沿DE折起,使A至A′处,且面A′DE⊥面CDE,△B′CE和△A′DE在面CDE的同侧.

(Ⅰ) 求证:B′C⊥平面CDE;
(Ⅱ) 求平面B′A′D与平面CDE所构成的锐二面角的余弦值.

(Ⅰ) 求证:B′C⊥平面CDE;
(Ⅱ) 求平面B′A′D与平面CDE所构成的锐二面角的余弦值.
分析:(Ⅰ)在原平面图形中,利用根据变的关系利用勾股定理得到BC⊥CE,即立体图中B′C⊥CE,结合已知B′C⊥DE,利用线面垂直的判定定理可得结论;
(Ⅱ)以C为原点,CE为y轴,CB为z轴建立空间直角坐标系,然后求出平面B′A′D与平面CDE的法向量,利用法向量所成角的余弦值得平面B′A′D与平面CDE所构成的锐二面角的余弦值.
(Ⅱ)以C为原点,CE为y轴,CB为z轴建立空间直角坐标系,然后求出平面B′A′D与平面CDE的法向量,利用法向量所成角的余弦值得平面B′A′D与平面CDE所构成的锐二面角的余弦值.
解答: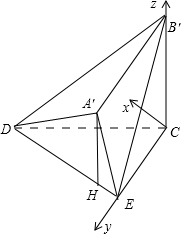 (Ⅰ)证明:如图,在直角梯形ABCD中,由,△CDE是边长为2的等边三角形,AB=5,
(Ⅰ)证明:如图,在直角梯形ABCD中,由,△CDE是边长为2的等边三角形,AB=5,
得:AD=
,BC=2
,CE=2,BE=4,
所以BC2+CE2=(2
)2+22=16=BE2.
即B′C⊥CE,又B′C⊥DE,DE∩CE=E,所以B′C⊥平面CDE.
(Ⅱ)解:以C为原点,CE为y轴,CB为z轴建立空间直角坐标系,
则C(0,0,0),B′(0,0,2
),D(
,1,0),E(0,2,0)
作A′H⊥DE,因为面A′DE⊥面CDE,所以A′H⊥面CDE,且A′H=
.
在平面图形中可求解得:H(
,
,0),所以A′(
,
,
).
易知面CDE的法向量
=(0,0,1),
设面PAD的法向量为
=(x,y,z),且
=(
,1,-2
),
=(
,
,-
).
由
,则
,取y=2,得x=
,z=
,
所以
=(
,2,
).
所以cos<
,
>=
=
=
.
所以平面B′A′D与平面CDE所构成的锐二面角的余弦值为
.
 (Ⅰ)证明:如图,在直角梯形ABCD中,由,△CDE是边长为2的等边三角形,AB=5,
(Ⅰ)证明:如图,在直角梯形ABCD中,由,△CDE是边长为2的等边三角形,AB=5,得:AD=
| 3 |
| 3 |
所以BC2+CE2=(2
| 3 |
即B′C⊥CE,又B′C⊥DE,DE∩CE=E,所以B′C⊥平面CDE.
(Ⅱ)解:以C为原点,CE为y轴,CB为z轴建立空间直角坐标系,
则C(0,0,0),B′(0,0,2
| 3 |
| 3 |
作A′H⊥DE,因为面A′DE⊥面CDE,所以A′H⊥面CDE,且A′H=
| ||
| 2 |
在平面图形中可求解得:H(
| ||
| 4 |
| 7 |
| 4 |
| ||
| 4 |
| 7 |
| 4 |
| ||
| 2 |
易知面CDE的法向量
| n1 |
设面PAD的法向量为
| n2 |
| B′D |
| 3 |
| 3 |
| B′A′ |
| ||
| 4 |
| 7 |
| 4 |
3
| ||
| 2 |
由
|
|
4
| ||
| 3 |
| 3 |
所以
| n2 |
4
| ||
| 3 |
| 3 |
所以cos<
| n1 |
| n2 |
| ||||
|
|
| ||||||||
1•
|
| 3 |
| 37 |
| 37 |
所以平面B′A′D与平面CDE所构成的锐二面角的余弦值为
3
| ||
| 37 |
点评:本题考查了线面垂直的判定,考查了利用空间向量求二面角的大小,综合考查了学生的空间想象能力和计算能力,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•浙江模拟)函数f(x)=Asin(ωx+φ)(A>0,ω>),|φ|<
(2013•浙江模拟)函数f(x)=Asin(ωx+φ)(A>0,ω>),|φ|< (2013•浙江模拟)如图,在四边形ABCD中,AB⊥BC,AD⊥DC.若|
(2013•浙江模拟)如图,在四边形ABCD中,AB⊥BC,AD⊥DC.若|