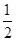题目内容
设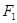 、
、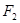 为双曲线
为双曲线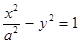 的两个焦点,点
的两个焦点,点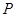 在此双曲线上,
在此双曲线上,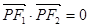 ,如果此双曲线的离心率等于
,如果此双曲线的离心率等于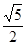 ,那么点
,那么点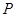 到
到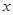 轴的距离等于 .
轴的距离等于 .
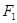 、
、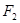 为双曲线
为双曲线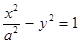 的两个焦点,点
的两个焦点,点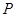 在此双曲线上,
在此双曲线上,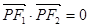 ,如果此双曲线的离心率等于
,如果此双曲线的离心率等于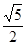 ,那么点
,那么点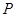 到
到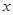 轴的距离等于 .
轴的距离等于 .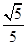
试题分析:解法一: ∵
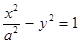 的离心率等于
的离心率等于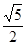 ,
,∴
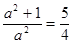 .
.∴
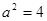 .
.∵
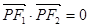 ,
,∴
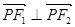 .
.∴
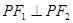 .
.∵点
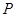 在双曲线
在双曲线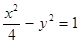 上,
上,∴
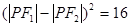 .
.∴
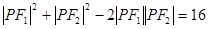 .
.∴
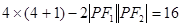 .
.∴
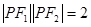 .
.设点
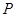 到
到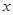 轴的距离等于
轴的距离等于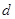 ,则
,则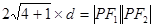 .
.∴
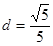 .
.解法二(方程思想):∵
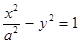 ,∴
,∴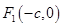 ,
,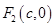 .
.∵
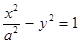 的离心率等于
的离心率等于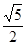 ,∴
,∴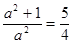 ,
,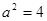 ,
,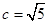 .
.∴,双曲线方程为
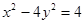 .
.设
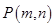 ,则
,则 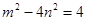 ①
①由
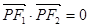 得
得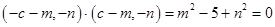 ②
②解得
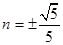 ,从而点
,从而点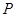 到
到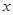 轴的距离等于
轴的距离等于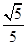 .
.
练习册系列答案
相关题目
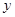 轴上,且过点
轴上,且过点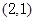 .
.
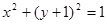 相切的直线
相切的直线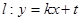 交抛物线于不同的两点
交抛物线于不同的两点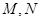 若抛物线上一点
若抛物线上一点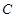 满足
满足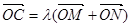
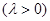 ,求
,求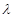 的取值范围.
的取值范围.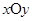 中,经过点
中,经过点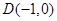 的动直线
的动直线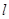 ,与椭圆
,与椭圆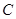 :
: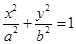 (
(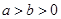 )相交于
)相交于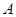 ,
,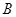 两点. 当
两点. 当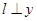 轴时,
轴时,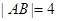 ,当
,当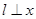 轴时,
轴时,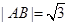 .
.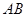 的中点为
的中点为 ,且
,且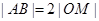 ,求直线
,求直线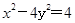 的离心率为( )
的离心率为( )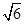
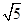
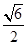
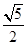
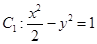 ,曲线
,曲线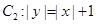 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与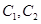 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.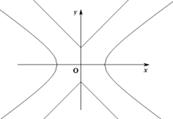
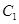 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);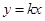 与
与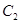 有公共点,求证
有公共点,求证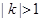 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;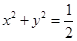 内的点都不是“C1—C2型点”.
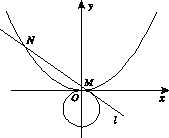
内的点都不是“C1—C2型点”.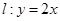 上一点
上一点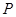 作圆
作圆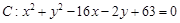 的切线
的切线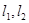 ,若
,若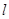 对称,则点
对称,则点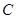 的距离为 .
的距离为 .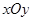 中,已知
中,已知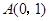 ,
,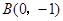 ,
,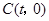 ,
,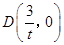 ,其中
,其中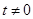 .设直线
.设直线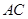 与
与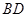 的交点为
的交点为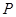 ,求动点
,求动点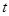 为参数)及普通方程.
为参数)及普通方程.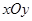 中,直线
中,直线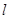 的方程为
的方程为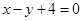 ,曲线
,曲线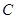 的参数方程为
的参数方程为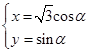 (
(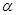 为参数).
为参数).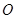 为极点,以
为极点,以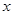 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点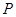 的极坐标为(4,
的极坐标为(4,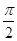 ),判断点
),判断点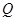 是曲线
是曲线