题目内容
[2014·河南洛阳模拟]下列命题中的假命题是( )
| A.?x∈R,2x-1>0 | B.?x∈N*,(x-1)2>0 |
| C.?x∈R,lgx<1 | D.?x∈R,tanx=2 |
B
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题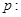 对任意
对任意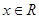 ,总有
,总有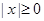 ;
;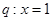 是方程
是方程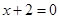 的根
的根
则下列命题为真命题的是
A.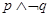 | B.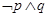 | C.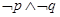 | D.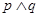 |
命题“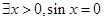 ”的否定为( )
”的否定为( )
A.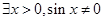 | B.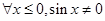 |
C. | D.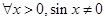 |
(5分)(2011•天津)设集合A={x∈R|x﹣2>0},B={x∈R|x<0},C={x∈R|x(x﹣2)>0},则“x∈A∪B”是“x∈C”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.即不充分也不必要条件 |
已知a∈R,且a≠0,则 是“a>1”的( ).
是“a>1”的( ).
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分又非必要条件 |
(3分)(2011•重庆)“x<﹣1”是“x2﹣1>0”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
对于任意实数x,〈x〉表示不小于x的最小整数,例如〈1.1〉=2,〈-1.1〉=-1,那么“|x-y|<1”是“〈x〉=〈y〉”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
(2011•湖北)若实数a,b满足a≥0,b≥0,且ab=0,则称a与b互补,记φ(a,b)=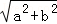 ﹣a﹣b那么φ(a,b)=0是a与b互补的( )
﹣a﹣b那么φ(a,b)=0是a与b互补的( )
| A.必要不充分条件 | B.充分不必要的条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设m,n表示不同的直线,α,β表示不同的平面,且m,n?α.则“α∥β”是“m∥β且n∥β”的( )
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |