题目内容
(本小题满分12分) 已知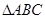 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是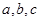 ,
,
设向量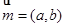 ,
, 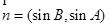 ,
, 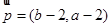
(Ⅰ)若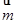 ∥
∥ ,求证:
,求证: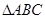 为等腰三角形;
为等腰三角形;
(Ⅱ)若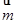 ⊥
⊥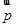 ,边长
,边长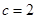 ,
,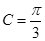 ,求
,求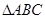 的面积.
的面积.
【答案】
(Ⅰ)利用正弦定理由角化边可以得到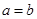 ,命题即得证.(Ⅱ)
,命题即得证.(Ⅱ)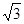
【解析】
试题分析:(Ⅰ) 证明: ∵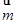 ∥
∥ , ∴
, ∴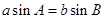 ,由正弦定理可知,
,由正弦定理可知,
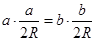 ,其中R是
,其中R是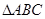 外接圆的半径,
外接圆的半径,
∴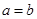 .
.
因此,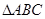 为等腰三角形.
为等腰三角形.
(Ⅱ)由题意可知,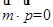 ,即
,即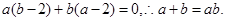
由余弦定理可知,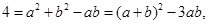 即
即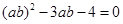
 ,(
,(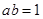 舍去)
舍去)
∴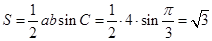 .
.
考点:正弦定理 余弦定理 面积公式 向量运算
点评:此题综合考查了三角形的面积公式,余弦定理,正弦定理以及向量运算,属基础题..

练习册系列答案
相关题目