题目内容
11.设i是虚数单位,$\overline{z}$是复数z的共轭复数,若z$•\overline{z}$=2($\overline{z}$+i),则z=( )| A. | -1-i | B. | 1+i | C. | -1+i | D. | 1-i |
分析 设出复数z=a+bi(a,b∈R),代入z•$•\overline{z}$=2($\overline{z}$+i)后整理,利用复数相等的条件列关于a,b的方程组求解a,b,则复数z可求.
解答 解:设z=a+bi(a,b∈R),则$\overline{z}$=a-bi,
由z$•\overline{z}$=2($\overline{z}$+i),得(a+bi)(a-bi)=2[a+(b-1)i],
整理得a2+b2=2a+2(b-1)i.
则$\left\{\begin{array}{l}b-1=0\\{a}^{2}+{b}^{2}=2a\end{array}\right.$,解得$\left\{\begin{array}{l}a=1\\ b=1\end{array}\right.$.
所以z=1+i.
故选B.
点评 本题考查了复数代数形式的混合运算,考查了复数相等的条件,两个复数相等,当且仅当实部等于实部,虚部等于虚部,是基础题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
2.从标有1,2,3,4,5,6的6张纸片中任取2张,那么这2张纸片数字之积为6的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{15}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{3}$ |
16.已知点A,B是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的顶点,P为双曲线上除顶点外的一点,记kPA,kPB分别表示直线PA,PB的斜率,若kPA•kPB=$\frac{5}{4}$,则该双曲线的离心率为( )
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.若直线ax-by+2=0(a>0,b>0)过圆C:x2+y2+2x-4y+1=0的圆心,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$+$\sqrt{2}$ | D. | $\frac{3}{2}$+2$\sqrt{2}$ |
19.若复数z满足(3-4i)z=5+10i,其中i为虚数单位,则z的虚部为( )
| A. | -2 | B. | 2 | C. | -2i | D. | 2i |
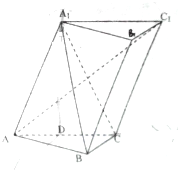 已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,BA1⊥AC1.
已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,BA1⊥AC1.