题目内容
已知点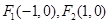 分别是椭圆
分别是椭圆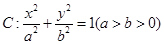 的左、右焦点, 点
的左、右焦点, 点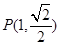 在椭圆上
在椭圆上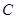 上.
上.
(Ⅰ)求椭圆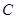 的标准方程;
的标准方程;
(Ⅱ)设直线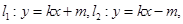 若
若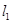 、
、 均与椭圆
均与椭圆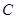 相切,试探究在
相切,试探究在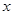 轴上是否存在定点
轴上是否存在定点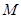 ,点
,点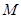 到
到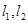 的距离之积恒为1?若存在,请求出点
的距离之积恒为1?若存在,请求出点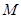 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
(1)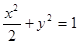 ;(2)满足题意的定点
;(2)满足题意的定点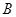 存在,其坐标为
存在,其坐标为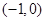 或
或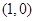
解析试题分析:本题主要考查椭圆的定义和标准方程以及直线与椭圆的位置关系等数学知识,考查分析问题解决问题的能力和计算能力.第一问,法一:利用焦点坐标求出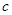 ,由于点
,由于点 在椭圆上,得到方程
在椭圆上,得到方程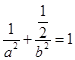 ,又因为
,又因为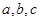 三个参量的关系得
三个参量的关系得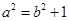 ,联立,解出
,联立,解出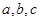 ,从而得到椭圆的方程;法二:利用椭圆的定义,
,从而得到椭圆的方程;法二:利用椭圆的定义,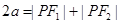 ,利用两点间的距离公式计算得出
,利用两点间的距离公式计算得出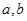 的值,从而得到椭圆的方程;第二问,直线
的值,从而得到椭圆的方程;第二问,直线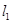 与椭圆联立,由于它们相切,所以方程只有一个根,所以
与椭圆联立,由于它们相切,所以方程只有一个根,所以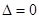 ,同理直线
,同理直线 与椭圆联立得到表达式
与椭圆联立得到表达式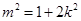 ,假设存在点
,假设存在点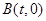 ,利用点到直线的距离,列出表达式,将
,利用点到直线的距离,列出表达式,将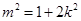 代入整理,使得到的表达式,解出
代入整理,使得到的表达式,解出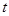 的值,从而得到
的值,从而得到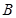 点坐标.
点坐标.
试题解析:(1)法一:由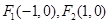 ,得
,得 , 1分
, 1分 2分
2分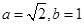 ∴椭圆
∴椭圆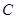 的方程为
的方程为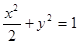 4分
4分
法二:由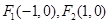 ,得
,得 , 1分
, 1分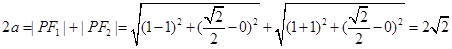 3分
3分
∴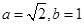
∴椭圆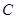 的方程为
的方程为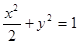 4分
4分
(2)把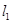 的方程代入椭圆方程得
的方程代入椭圆方程得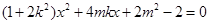 5分
5分
∵直线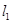 与椭圆
与椭圆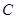 相切,∴
相切,∴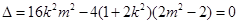 ,化简得
,化简得 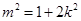 同理把
同理把 的方程代入椭圆方程也得:
的方程代入椭圆方程也得: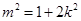 7分
7分
设在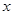 轴上存在点
轴上存在点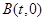 ,点
,点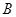 到直线
到直线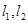 的距离之积为1,则
的距离之积为1,则  ,即
,即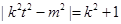 , 9分
, 9分
把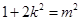 代入并去绝对值整理,
代入并去绝对值整理, 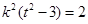 或者
或者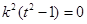 10分
10分
前式显然不恒成立;而要使得后式对任意的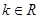 恒成立 则
恒成立 则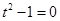 ,解得
,解得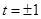 ;
;
综上所述,满足题意的定点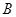 存在,其坐标为
存在,其坐标为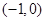 或
或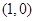 12分
12分
考点:1.椭圆的标准方程;2.椭圆的定义;3.两点间的距离公式;4.点到直线的距离公式.

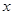 轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.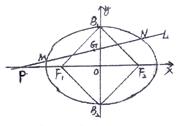
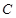 的顶点在坐标原点
的顶点在坐标原点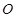 ,对称轴为
,对称轴为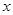 轴,焦点为
轴,焦点为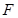 ,抛物线上一点
,抛物线上一点 的横坐标为2,且
的横坐标为2,且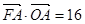 .
.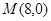 作直线
作直线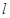 交抛物线于
交抛物线于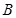 ,
,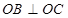 .
.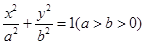 的左、右焦点分别为
的左、右焦点分别为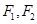 ,离心率为
,离心率为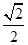 ,P是椭圆上一点,且
,P是椭圆上一点,且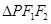 面积的最大值等于2.
面积的最大值等于2.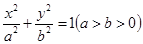 的左、右焦点和短轴的一个端点构成边长为4的正三角形.
的左、右焦点和短轴的一个端点构成边长为4的正三角形.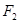 的直线
的直线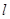 与椭圆C相交于A、B两点,若
与椭圆C相交于A、B两点,若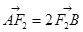 ,求直线
,求直线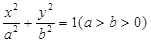 上的点
上的点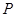 到左右两焦点
到左右两焦点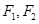 的距离之和为
的距离之和为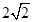 ,离心率为
,离心率为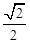 .
.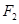 的直线
的直线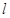 交椭圆于
交椭圆于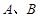 两点,若
两点,若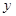 轴上一点
轴上一点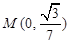 满足
满足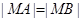 ,求直线
,求直线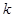 的值.
的值.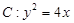 的焦点为
的焦点为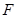 ,过点
,过点 交抛物线
交抛物线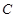 于点
于点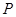 ,
,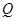 .
.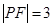 (点
(点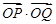 为定值(点
为定值(点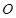 为坐标原点).
为坐标原点).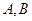 是抛物线
是抛物线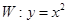 上的两个点,点
上的两个点,点 的坐标为
的坐标为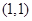 ,直线
,直线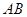 的斜率为k,
的斜率为k,  为坐标原点.
为坐标原点.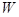 的焦点在直线
的焦点在直线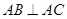 ,过
,过 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为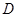 ,求
,求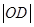 的最小值.
的最小值.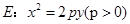 ,直线
,直线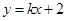 与E交于A、B两点,且
与E交于A、B两点,且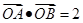 ,其中O为原点.
,其中O为原点.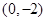 ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为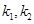 ,证明:
,证明: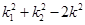 为定值.
为定值.