题目内容
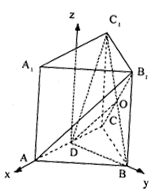
(08年西工大附中理)如图,已知正三棱柱ABC- ![]() ,D是AC的中点,∠
,D是AC的中点,∠![]() DC = 60°
DC = 60°
(Ⅰ)求证:A![]() ∥平面B
∥平面B![]() D;
D;
(Ⅱ)求二面角D-B![]() -C的大小。
-C的大小。

解析:解法一:
 (Ⅰ)连结B1C交BC
(Ⅰ)连结B1C交BC![]() 于O,则O是B
于O,则O是B![]() C的中点,连结DO。
C的中点,连结DO。
∵在△A![]() C中,O、D均为中点,
C中,O、D均为中点,
∴A![]() ∥DO …………………………2分
∥DO …………………………2分
∵A![]()
![]() 平面B
平面B![]() D,DO
D,DO![]() 平面B
平面B![]() D,
D,
∴A![]() ∥平面B
∥平面B![]() D。…………………4分
D。…………………4分
(Ⅱ)设正三棱柱底面边长为2,则DC = 1。
∵∠![]() DC = 60°,∴C
DC = 60°,∴C![]() =
= ![]() 。
。
作DE⊥BC于E。
∵平面BC![]() ⊥平面ABC,
⊥平面ABC,
∴DE⊥平面BC![]()
![]()
作EF⊥B![]() 于F,连结DF,则 DF⊥B
于F,连结DF,则 DF⊥B![]()
∴∠DFE是二面角D-B![]() -C的平面角……………………………………8分
-C的平面角……………………………………8分
在Rt△DEC中,DE=![]()
在Rt△BFE中,EF = BE?sin![]()
∴在Rt△DEF中,tan∠DFE = ![]()
 ∴二面角D-B
∴二面角D-B![]() -C的大小为arctan
-C的大小为arctan![]() ………………12分
………………12分
解法二:以AC的中D为原点建立坐标系,如图,
设| AD | = 1∵∠![]() DC =60°∴| C
DC =60°∴| C![]() | =
| = ![]() 。
。
则A(1,0,0),B(0,![]() ,0),C(-1,0,0),
,0),C(-1,0,0),
![]() (1,0
(1,0![]() ),
),![]() ,
,![]()
(Ⅰ)连结![]() C交B
C交B![]() 于O是
于O是![]() C的中点,连结DO,则 O
C的中点,连结DO,则 O .
. ![]() =
=![]()
∵A![]()
![]() 平面B
平面B![]() D,
D,
∴A![]() ∥平面B
∥平面B![]() D.……………………………………………………………4分
D.……………………………………………………………4分
(Ⅱ)![]() =(-1,0,
=(-1,0,![]() ),
),![]()
设平面B![]() D的法向量为n = ( x , y , z ),则
D的法向量为n = ( x , y , z ),则![]()
即 则有
则有![]() = 0令z = 1
= 0令z = 1
则n = (![]() ,0,1)…………………………………………………………8分
,0,1)…………………………………………………………8分
设平面BC![]()
![]() 的法向量为m = ( x′ ,y′,z′)
的法向量为m = ( x′ ,y′,z′)
![]() =(0,0,
=(0,0,![]() ),,
),,![]()

令y = -1,解得m = (![]() ,-1,0)
,-1,0)
二面角D ―B![]() ―C的余弦值为cos<n , m>=
―C的余弦值为cos<n , m>=![]()

