题目内容
（08年西工大附中理）函数
过曲线y=f(x)上的点P(1,f(1))处的切线方程为y=3x+1
（1）若y=f(x)在x=-2时有极值，求f(x)的表达式；
（2）若函数y=f(x)在区间
上单调递增，求b的取值范围.
解析： 由
求导数得
，过y=f(x)上点P（1，f(1)）处的切线方程为：
即y-(a+b+c+1)=(3+2a+b)(x-1),而过y=f(x)上P（1,f(1)）的切线方程为：y=3x+1,故
即
y=f(x)在x=-2时有极值，故
由
相联立解得
，
（2）
在区间
上单调递增
又
，由（1）知
依题意
在上恒有
，即
在上恒成立.
①在
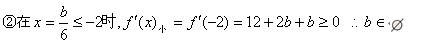
③在
综合上述讨论可知，所求参数b取值范围是：b≥0……（14分）
练习册系列答案
名师金手指领衔课时系列答案
相关题目
，D是AC的中点，∠
DC = 60°
∥平面B
抽检规则是这样的：一次取一件产品检查，若前三次没有抽查到次品，则用户接收这箱产品，而前三次中只要抽查到次品就停止抽检，并且用户拒绝接收这箱产品
的右准线与一条渐近线交于点M，F是右焦点，若
，且双曲线C的离心率e=
.
且
，求直线l斜率k的取值范围
中，底面
是一直角梯形，
，
，
，
，且
平面
与底面成
角．
平面
；
的大小；
，
为垂足，求异面直线
与
所成角的大小． 