题目内容
在△ABC中，已知角A、B、C所对的边分别为a、b、c，直l1：ax+y+1=0与直线l2：（b2+c2-bc）x+ay+4=0互相平行（其中a≠4）
（I）求角A的值，
（II）若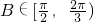
，求
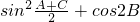的取值范围．
解：（I）l1∥l2，得a2=b2+c2-bc（a≠4）
即b2+c2-a2=bc…（2分）∴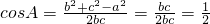
∵A∈（0，π），∴
．…（5分）
（II）
=
=
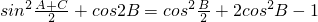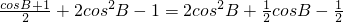…（8分）∵，∴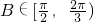
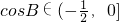…（9分）∴
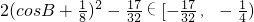…（11分）
即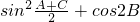的取值范围为
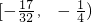…（12分）
分析：（I）利用直线平行，推出a2=b2+c2-bc（a≠4），结合余弦定理，即可求角A的值，
（II）利用二倍角公式以及配方法化简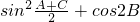为二次函数的平方式，通过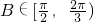推出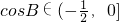，然后求出表达式的取值范围．
点评：本题是中档题考查直线的平行条件的应用，余弦定理二倍角公式配方法求函数的最值，考查计算能力．
即b2+c2-a2=bc…（2分）∴
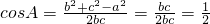∵A∈（0，π），∴．…（5分）（II）
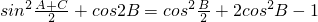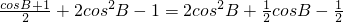==…（8分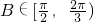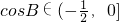）∵，∴…（9分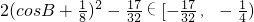）∴…（11分）即
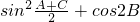的取值范围为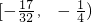…（12分）分析：（I）利用直线平行，推出a2=b2+c2-bc（a≠4），结合余弦定理，即可求角A的值，
（II）利用二倍角公式以及配方法化简
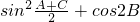为二次函数的平方式，通过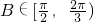推出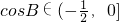，然后求出表达式的取值范围．点评：本题是中档题考查直线的平行条件的应用，余弦定理二倍角公式配方法求函数的最值，考查计算能力．
练习册系列答案
相关题目