题目内容
如图2-4-18(1),四边形ABCD是⊙O的内接四边形,A是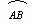
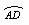
(1) (2)
图2-4-18
(1)求证:AB·DA=CD·BE;
(2)如图2-4-18(2),若点E在CB延长线上运动,使切线EA变为割线EFA,其他条件不变,问具备什么条件使原结论成立?
思路分析:(1)只需证△ABE∽△CDA.?
(2)如题图(2),要使结论仍然成立,注意到∠ABE =∠ADC始终成立,因此仍然只需使△ABE∽△CDA即可,这样只要另一组对应角相等即可,即只需∠BAE =∠ACD或∠E =∠CAD.
(1)证明:连结AC,∵AE切⊙O于A,?
∴∠EAB =∠ACB.?
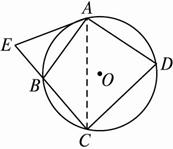
∵![]() =
=![]() ,?
,?
∴∠ACD =∠ACB.?
∴∠EAB =∠ACD.?
又∵四边形ABCD内接于⊙O,?
∴∠ABE =∠CDA.∴△ABE∽△CDA.?
∴![]() =
=![]() .∴AB·DA =CD·BE.
.∴AB·DA =CD·BE.
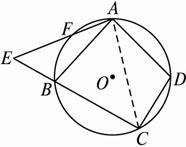
(2)解:当![]() =
=![]() 时,∠EAB =∠ACD,
时,∠EAB =∠ACD,
又∠ABE =∠ADC,?
∴△ABE∽△ACD,?
∴AB·DA =CD·BE,此时仍然成立.

练习册系列答案
相关题目

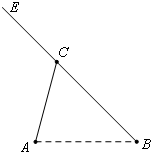 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.