题目内容
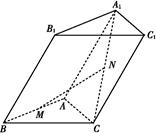
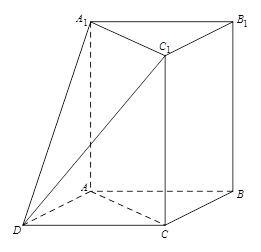
如图,四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形, ,
, 平面
平面 ,
, ,
, ,
, 是
是 的中点.
的中点.
(1)求证: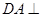 平面
平面 ;
;
(2)若以 为坐标原点,射线
为坐标原点,射线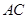 、
、 、
、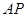 分别是
分别是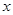 轴、
轴、 轴、
轴、 轴的正半轴,建立空间直角坐标系,已经计算得
轴的正半轴,建立空间直角坐标系,已经计算得 是平面
是平面 的法向量,求平面
的法向量,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)参考解析;(2)
解析试题分析:(1)需证明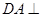 平面
平面 ,转化为证明AD⊥AC,AD⊥PA.因为PA垂直平面ABCD,由题意可得AD⊥AC,AD⊥PA显然成立,即可得结论.
,转化为证明AD⊥AC,AD⊥PA.因为PA垂直平面ABCD,由题意可得AD⊥AC,AD⊥PA显然成立,即可得结论.
(2)如图建立空间直角坐标系,因为 是平面
是平面 的法向量,所以求出平面PAF的法向量
的法向量,所以求出平面PAF的法向量 ,再根据两平面的法向量的夹角的余弦值,即可得到平面
,再根据两平面的法向量的夹角的余弦值,即可得到平面 与平面
与平面 所成锐二面角的余弦值,
所成锐二面角的余弦值,
试题解析: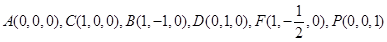 . (1) 证明方法一:
. (1) 证明方法一: 四边形是平行四边形,
四边形是平行四边形,
 平面
平面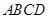

 ,又
,又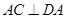 ,
, ,
,
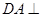 平面
平面 .
.
方法二:证得 是平面
是平面 的一个法向量,
的一个法向量,
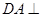 平面
平面 .
.
(2)通过平面几何图形性质或者解线性方程组,计算得平面 一个法向量为
一个法向量为 ,
,
又平面 法向量为
法向量为 ,所以
,所以
 所求二面角的余弦值为
所求二面角的余弦值为 .
.
考点:1.线面垂直的证明2.二面角.3.空间向量的运算.4.运算的能力.

练习册系列答案
相关题目
 中,底面ABCD和侧面
中,底面ABCD和侧面 都是矩形,E是CD的中点,
都是矩形,E是CD的中点,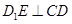 ,
,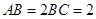 .
. ;
;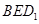 所成的锐二面角的大小为
所成的锐二面角的大小为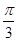 ,求线段
,求线段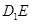 的长度.
的长度.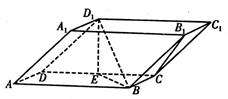
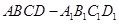 中,
中, 是
是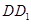 的中点.
的中点. 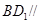 平面
平面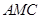 ;
;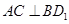 ;
;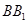 上是否存在点
上是否存在点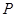 ,当
,当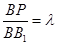 时,平面
时,平面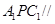 平面
平面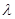 的值并证明;若不存在,请说明理由.
的值并证明;若不存在,请说明理由.
 中,
中, 平面
平面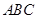 ,
,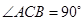 ,
,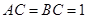 ,
,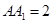 .以
.以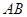 ,
, 为邻边作平行四边形
为邻边作平行四边形 ,连接
,连接 和
和 .
.
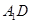 ∥平面
∥平面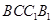 ;
;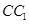 与平面
与平面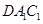 所成角的正弦值;
所成角的正弦值; ,使平面
,使平面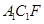 垂直?若存在,求出
垂直?若存在,求出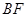 的长;若
的长;若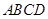 中,
中, ,
, ,且
,且 ,以BD为折线,把△ABD折起,
,以BD为折线,把△ABD折起, ,连接AC.
,连接AC.
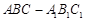 中,
中,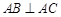 ,顶点
,顶点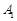 在底面
在底面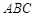 上的射影恰为点
上的射影恰为点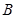 ,
,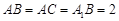 .
.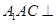 平面
平面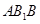 ;
; 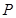 为
为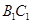 的中点,求出二面角
的中点,求出二面角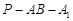 的余弦值.
的余弦值.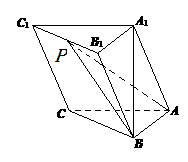
 为
为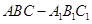 中,
中, 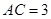 ,
, 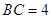 ,
,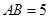 ,点
,点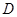 是
是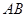 的中点.四面体
的中点.四面体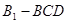 的体积是
的体积是 ,求异面直线
,求异面直线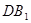 与
与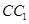 所成的角.
所成的角.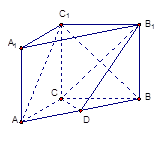
 中,侧面
中,侧面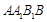 为菱形,且
为菱形,且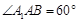 ,
,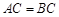 ,
, 是
是 的中点.
的中点.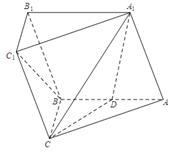
 平面
平面 ;
; ∥平面
∥平面 .
. A1B1C1,
A1B1C1,