题目内容
设抛物线y2=2px(p> 0)的焦点为F,经过点F的直线交抛物线于A、B两点.点C在抛物线的准线上,且BC∥x轴.证明直线 AC经过原点O.
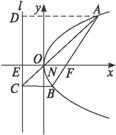
思路解析:本题的解法很多,采用坐标方法进行代数推理,可以证明OA与OC的斜率相等,证明AO+OC=AC,证明OC与BF的交点A在抛物线上,证明AC的方程形如y=φ(p)x,等等,每种证明又有不同的表述形式,甚至可以用参数方程法,采用平面几何方法进行推理. 证法一:如图所示, 因为抛物线y2=2px(p>0)的焦点为F( 若记A(x1,y1),B(x2,y2),则y1,y2是该方程的两个根,所以y1y2=-p2. 因为BC∥x轴,且点C在准线x=- 故直线CO的斜率为 k= 即k也是直线OA的斜率,所以直线AC经过原点O. 证法二:设A(x1,y1),B(x2,y2). 因为BC∥x轴,所以C(- 因为A、B在抛物线上, 所以y12=2px1,y22=2px2. 又因为直线AB过焦点F, 所以kAF=kBF,即 所以 所以y1y2(y2-y1)=p2(y1-y2). 因为y1≠y2,所以y1y2=-p2. 因为kOC= 所以直线AC经过原点O. 证法三:因为抛物线y2=2px(p>0)的焦点为( 所以设直线AB的方程为x=ky+ 由 消去x得y2-2pky-p2=0. 所以yA·yB=-p2. 因为A( 所以直线AC的方程为 化简得y= 显然,原点O适合此方程,所以原点O在直线AC上. 证法四:设B(a,b),则C(- 所以直线BF的方程为y(a- 直线OC的方程为y=- 所以 消y得- 所以 因为B在抛物线y2=2px上,所以b2=2ap. 所以A′( 所以(- 所以A′在抛物线y2=2px上.所以A′与A重合,即直线AC经过原点O. 证法五:如下图所示,记x轴与抛物线准线l的交点为E,过A作AD⊥l,D是垂足,则AD∥FE∥BC. 连结AC,与EF相交于点N,则 根据抛物线的性质,得|AF|=|AD|,|BF|=|BC|. 所以|EN|= 即点N是EF的中点,与抛物线的顶点O重合,所以直线AC经过原点O. 证法六:如下图所示, 设准线交x轴于点E,过A点作AM⊥x轴于M. 设A(x1,y1),B(x2,y2),则C(- 由证法二知y1= 又 所以 故A、O、C三点共线,即直线AC过原点O.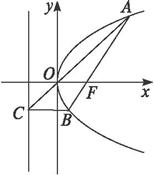
![]() ,0),所以经过点F的直线AB的方程可设为x=my+
,0),所以经过点F的直线AB的方程可设为x=my+![]() ,代入抛物线方程得y2-2pmy-p2=0.
,代入抛物线方程得y2-2pmy-p2=0.![]() 上,所以点C的坐标为(-
上,所以点C的坐标为(-![]() ,y2).
,y2).![]() =
=![]() =
=![]() ,
,![]() ,y2).
,y2).![]() =
=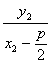 .
.![]() .
.![]() =
=![]() =
=![]() =
=![]() =kOA,
=kOA,![]() ,0),
,0),![]() .
.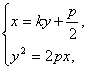
![]() ,yA),C(-
,yA),C(-![]() ,yB),即C(-
,yB),即C(-![]() ,-
,-![]() ),
), =
=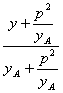 .
.![]() x.
x.![]() ,b),F(
,b),F(![]() ,0),
,0),![]() )=b(x-
)=b(x-![]() ),
),![]() x.
x.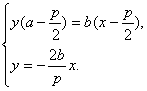
![]() x(a-
x(a-![]() )=b(x-
)=b(x-![]() ).
).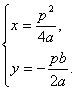 所以A′(
所以A′(![]() ,-
,-![]() ).
).![]() ,-
,-![]() ).
).![]() )2=
)2=![]() =2p·
=2p·![]() .
.
![]() ,
,![]() .
.![]() =
=![]() =|NF|,
=|NF|,
![]() ,y2),所以
,y2),所以![]() =
=![]() .
.![]() ,
,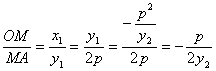 ,
,![]() =
=![]() .所以△AOM∽△COE.所以∠AOM=∠COE.
.所以△AOM∽△COE.所以∠AOM=∠COE.

寒假生活20天系列答案
寒假生活江西高校出版社系列答案
寒假生活三秦出版社系列答案
寒假生活上海专用系列答案
寒假生活阳光出版社系列答案
寒假生活指导系列答案
寒假特训系列答案
BEST学习丛书提升训练寒假湖南师范大学出版社系列答案
寒假提优捷径系列答案
寒假新动向系列答案
