题目内容

平面α，β，γ两两互相垂直，且交于点A，点B到α，β，γ的距离均为1，则A、B两点之间的距离|AB|=（　　）

A．1

B．

2

C．

3

D．2

分析：根据题意，以点B到α、β、γ的三条垂线段为长、宽、高作正方体，可得A、B两点之间的距离恰好等于该正方体的对角线长，结合正方体对角线公式可算出该距离．

解答：解：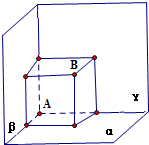

根据题意，可得
∵平面α、β、γ两两互相垂直，点B到α、β、γ的距离均为1
∴以点B到α、β、γ的三条垂线段为长、宽、高，作正方体如图所示
可得A、B两点之间的距离恰好等于该正方体的对角线长
∴|AB|=

12+12+12

=

3

故选：C

点评：本题给出两两互相垂直的三个平面，求点A、B之间的距离．着重考查了正方体的性质和空间距离的求法等知识，属于中档题．

练习册系列答案

状元训练法系列答案

新课标两导两练高效学案系列答案

金榜夺冠系列答案

期末复习百分百系列答案

标准单元测试卷系列答案

名校学案全能测评100分系列答案

天利38套对接中考单元专题双测卷系列答案

全程考评一卷通系列答案

课时金练系列答案

小学同步3练探究100分系列答案

相关题目

（2012•扬州模拟）已知两条不同的直线m、n与两个互异的平面α、β给出下列五个命题：
①若m∥α，n∥α，则m∥n；
②若m∥α，n⊥α，则m⊥n；
③若m⊥α，m∥β，则α⊥β；
④若m⊥α，α⊥β，则m∥β；
其中真命题的序号是．

在平面直角坐标系中，已知点A（1，0），点B在直线l：x=-1上运动，过点B与l垂直的直线和线段AB的垂直平分线相交于点M．
（1）求动点M的轨迹E的方程；
（2）过（1）中的轨迹E上的定点P（x₀，y₀）（y₀＞0）作两条直线分别与轨迹E相交于C（x₁，y₁），D（x₂，y₂）两点．试探究：当直线PC，PD的斜率存在且倾斜角互补时，直线CD的斜率是否为定值？若是，求出这个定值；若不是，说明理由．

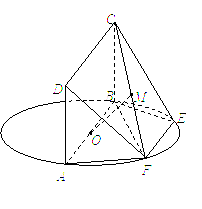（本小题满分12分）如图，为圆的直径，点、在

圆上，且，矩形所在的平面和圆所在的平面互

相垂直，且，.

（1）设的中点为，求证：平面；

（2）求直线CF与平面ADF所成角的大小。

（3）设平面将几何体分成的两个锥体的体积分

别为，，求．

已知两条不同的直线m、n与两个互异的平面α、β给出下列五个命题：
①若m∥α，n∥α，则m∥n；
②若m∥α，n⊥α，则m⊥n；
③若m⊥α，m∥β，则α⊥β；
④若m⊥α，α⊥β，则m∥β；
其中真命题的序号是．________．

已知两条不同的直线m、n与两个互异的平面α、β给出下列五个命题：
①若m∥α，n∥α，则m∥n；
②若m∥α，n⊥α，则m⊥n；
③若m⊥α，m∥β，则α⊥β；
④若m⊥α，α⊥β，则m∥β；
其中真命题的序号是．．