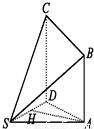
题目内容
如图所示,四棱锥S-ABCD中,底面ABCD是正方形,SA⊥面ABCD,且SA=AB,M、N分别为SB、SD中点,求证:
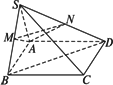
(1)DB∥平面AMN;
(2)SC⊥平面AMN.
答案:
解析:
解析:
|
证明:(1)∵M、N分别为SB、SD的中点,∴MN∥BD. ∴BD∥平面AMN. (2)∵SA⊥平面ABCD,AC⊥BD,∴SC⊥BD.∴SC⊥MN. 又∵CD⊥AD,SA⊥CD,∴CD⊥平面SAD.∴CD⊥AN. 又AN为等腰Rt△SAD斜边中线,∴AN⊥SD. ∴AN⊥平面SCD.∴AN⊥SC.∴SC⊥平面AMN. |

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图所示,四棱锥S-ABCD中,AB∥CD,CD⊥面SAD.且
如图所示,四棱锥S-ABCD中,AB∥CD,CD⊥面SAD.且 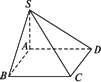
 如图所示,四棱锥S-ABCD中,AB∥CD,CD⊥面SAD.且
如图所示,四棱锥S-ABCD中,AB∥CD,CD⊥面SAD.且 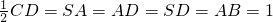 .
. .
.