题目内容
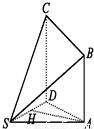
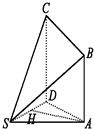 如图所示,四棱锥S-ABCD中,AB∥CD,CD⊥面SAD.且
如图所示,四棱锥S-ABCD中,AB∥CD,CD⊥面SAD.且 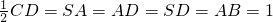 .
.
(1)当H为SD中点时,求证:AH∥平面SBC;平面SBC⊥平面SCD.
(2)求点D到平面SBC的距离.
解:(1)取SC中点G,连接HG、BG.
∵H为SD的中点,∴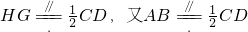 .
.
∴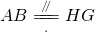 .故知四边形ABGH为平行四边形.∴AH∥BG,∴AH∥面SBC.
.故知四边形ABGH为平行四边形.∴AH∥BG,∴AH∥面SBC.
∵CD⊥面SAD,且CD?面SCD.
∴面SCD⊥面SAD,且交线为SD.
∵SA=AD=SD且SH=HD,∴AH⊥SD.
∴AH⊥面SCD,又AH∥BG,∴BG⊥面SCD,
又BG?面SBC.∴面SBC⊥面SCD.
(2)连接BD,设D到平面SBC的距离为h,则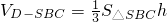 ,
,
又VD-SBC=VB-SDC,∴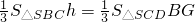 .
.
∴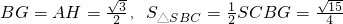 .
.
∵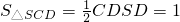 ,∴
,∴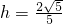 .
.
分析:(1)取SC中点G,连接HG、BG,由三角形中位线定理,H为SD的中点,可证明四边形ABGH为平行四边形,则AH∥BG,由线面平行的判定定理即可得到AH∥面SBC;由已知CD⊥面SAD,由线面垂直的判定定理可得BG⊥面SCD,最终由面面垂直的判定定理可得面SBC⊥面SCD;
(2)连接BD,设D到平面SBC的距离为h,h是三棱锥D-SBC的高,求出三角形SBC的面积,再利用换低公式和体积相等求出点D到平面SBC的距离即可.
点评:本小题主要考查直线与平面平行的判定、直线与平面垂直的判定、点、线、面间的距离计算等基础知识,考查空间想象力、化归与转化思想.属于基础题.
∵H为SD的中点,∴
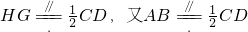 .
.∴
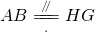 .故知四边形ABGH为平行四边形.∴AH∥BG,∴AH∥面SBC.
.故知四边形ABGH为平行四边形.∴AH∥BG,∴AH∥面SBC.∵CD⊥面SAD,且CD?面SCD.
∴面SCD⊥面SAD,且交线为SD.
∵SA=AD=SD且SH=HD,∴AH⊥SD.
∴AH⊥面SCD,又AH∥BG,∴BG⊥面SCD,
又BG?面SBC.∴面SBC⊥面SCD.
(2)连接BD,设D到平面SBC的距离为h,则
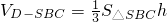 ,
,又VD-SBC=VB-SDC,∴
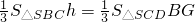 .
.∴
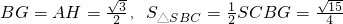 .
.∵
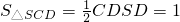 ,∴
,∴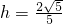 .
.分析:(1)取SC中点G,连接HG、BG,由三角形中位线定理,H为SD的中点,可证明四边形ABGH为平行四边形,则AH∥BG,由线面平行的判定定理即可得到AH∥面SBC;由已知CD⊥面SAD,由线面垂直的判定定理可得BG⊥面SCD,最终由面面垂直的判定定理可得面SBC⊥面SCD;
(2)连接BD,设D到平面SBC的距离为h,h是三棱锥D-SBC的高,求出三角形SBC的面积,再利用换低公式和体积相等求出点D到平面SBC的距离即可.
点评:本小题主要考查直线与平面平行的判定、直线与平面垂直的判定、点、线、面间的距离计算等基础知识,考查空间想象力、化归与转化思想.属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
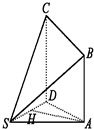 如图所示,四棱锥S-ABCD中,AB∥CD,CD⊥面SAD.且
如图所示,四棱锥S-ABCD中,AB∥CD,CD⊥面SAD.且 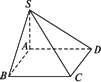
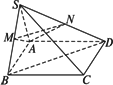
 .
.