题目内容
在△ABC中,若0<tanA•tanB<1,那么△ABC一定是( )A.锐角三角形
B.钝角三角形
C.直角三角形
D.形状不确定
【答案】分析:利用同角三角函数间的基本关系切化弦,变形后利用两角和与差的余弦函数公式化简,得到cos(A+B)的值大于0,可得出A+B为锐角,进而确定出C为钝角,得到三角形ABC为钝角三角形.
解答:解:∵0<tanA•tanB<1,
∴0<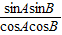 <1,即sinAsinB<cosAcosB,
<1,即sinAsinB<cosAcosB,
∴cosAcosB-sinAsinB=cos(A+B)>0,
∴0<A+B<90°,
则C>90°,即△ABC为钝角三角形.
故选B
点评:此题考查了三角形形状的判断,涉及的知识有:同角三角函数间的基本关系,两角和与差的余弦函数公式,以及余弦函数的图象与性质,熟练掌握公式及基本关系是解本题的关键.
解答:解:∵0<tanA•tanB<1,
∴0<
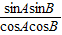 <1,即sinAsinB<cosAcosB,
<1,即sinAsinB<cosAcosB,∴cosAcosB-sinAsinB=cos(A+B)>0,
∴0<A+B<90°,
则C>90°,即△ABC为钝角三角形.
故选B
点评:此题考查了三角形形状的判断,涉及的知识有:同角三角函数间的基本关系,两角和与差的余弦函数公式,以及余弦函数的图象与性质,熟练掌握公式及基本关系是解本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
在△ABC中,若0<tanA?tanB<1,那么tanC的值( )
| A、恒大于0 | B、恒小于0 | C、可能为0 | D、可正可负 |