题目内容
3.在平面直角坐标系xOy中,已知椭圆C1:x2a2+y2b2=1(a>b>0)的左焦点为F1(-1,0)且点P(0,1)在C1上.(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
分析 (1)因为椭圆C1的左焦点为F1(-1,0),所以c=1,点P(0,1)代入椭圆x2a2+y2b2=1,得b=1,由此能求出椭圆C1的方程;
(2)设直线l的方程为y=kx+m,由{x22+y2=1y=kx+m,得(1+2k2)x2+4kmx+2m2-2=0.因为直线l与椭圆C1相切,所以△=16k2m2-4(1+2k2)(2m2-2)=0.再由直线和抛物线相切,联立方程,运用判别式为0,由此能求出直线l的方程.
解答 解:(1)因为椭圆C1的左焦点为F1(-1,0),所以c=1,
点P(0,1)代入椭圆x2a2+y2b2=1,得1b2=1,即b=1,
所以a2=b2+c2=2,
所以椭圆C1的方程为x22+y2=1;
(2)直线l的斜率显然存在,
设直线l的方程为y=kx+m,
由{x22+y2=1y=kx+m,消去y并整理得(1+2k2)x2+4kmx+2m2-2=0,
因为直线l与椭圆C1相切,
所以△=16k2m2-4(1+2k2)(2m2-2)=0
整理得2k2-m2+1=0①
由{y2=4xy=kx+m,消去y并整理得k2x2+(2km-4)x+m2=0,
因为直线l与抛物线C2相切,所以△=(2km-4)2-4k2m2=0,
整理得km=1②
综合①②,解得{k=√22m=√2或{k=−√22m=−√2,
所以直线l的方程为y=√22x+√2或y=-√22x-√2.
点评 本题考查椭圆方程的求法,考查直线与圆锥曲线的位置关系,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
11.两直线ax+by+4=0和(1-a)x-y-b=O都平行于x+2y+3=0,则( )
| A. | {a=23b=−3 | B. | {a=32b=−3 | C. | {a=−32b=3 | D. | {a=32b=3 |
15.已知直线l1,l2过椭圆x24+y243=1的中心且相互垂直的两条直线,分别交椭圆于A,B,C,D,四边形ABCD的面积的最小值是( )
| A. | 2 | B. | 4 | C. | 8√33 | D. | 16√33 |
13.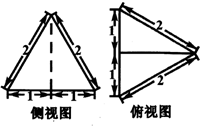 某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
 某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )| A. | 2 | B. | 3 | C. | 32 | D. | 52 |

 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=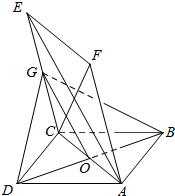 如图,已知边长为2的菱形ABCD与菱形ACEF全等,且∠FAC=∠ABC,平面ABCD⊥平面ACEF,点G为CE的中点.
如图,已知边长为2的菱形ABCD与菱形ACEF全等,且∠FAC=∠ABC,平面ABCD⊥平面ACEF,点G为CE的中点.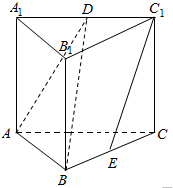 直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.
直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.