题目内容
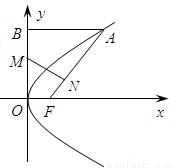
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为8且位于x轴上方的点. A到抛物线准线的距离等于10,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).(Ⅰ)求抛物线C的方程;
(Ⅱ)过M作MN⊥FA,垂足为N,求点N的坐标;
(Ⅲ)以M为圆心,4为半径作圆M,点P(m,0)是x轴上的一个动点,试讨论直线AP与圆M的位置关系.
【答案】分析:(Ⅰ)抛物线的准线为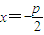 ,于是
,于是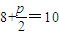 ,p=4,由此可知抛物线方程为y2=8x.
,p=4,由此可知抛物线方程为y2=8x.
(Ⅱ)由题意得B(0,8),M(0,4),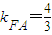 ,
,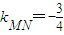 ,直线FA的方程为
,直线FA的方程为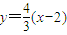 ,直线MN的方程为
,直线MN的方程为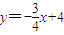 由此可知点N的坐标为
由此可知点N的坐标为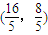 .
.
(Ⅲ)由题意得,圆M的圆心坐标为(0,4),半径为4.当m=8时,直线AP的方程为x=8,此时,直线AP与圆M相离;当m≠8时,直线AP的方程为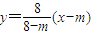 ,圆心M(0,4)到直线AP的距离
,圆心M(0,4)到直线AP的距离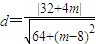 ,由此可判断直线AP与圆M的位置关系.
,由此可判断直线AP与圆M的位置关系.
解答:解:(Ⅰ)抛物线的准线为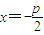 ,于是
,于是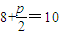 ,
,
∴p=4,∴抛物线方程为y2=8x(4分)
(Ⅱ)∵点A的坐标为(8,8),
由题意得B(0,8),M(0,4),又∵F(2,0),∴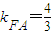 (6分)
(6分)
又MN⊥FA,∴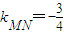 ,则直线FA的方程为
,则直线FA的方程为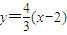 ,
,
直线MN的方程为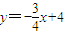 (8分)
(8分)
联立方程组,解得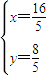 ,∴点N的坐标为
,∴点N的坐标为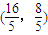 (10分)
(10分)
(Ⅲ)由题意得,圆M的圆心坐标为(0,4),半径为4.
当m=8时,直线AP的方程为x=8,此时,直线AP与圆M相离(12分)
当m≠8时,直线AP的方程为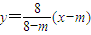 ,
,
即为8x-(8-m)y-8m=0,所以圆心M(0,4)到直线AP的距离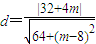 ,
,
令d>4,解得m>2;令d=4,解得m=2;令d<4,解得m<2(14分)
综上所述,当m>2时,直线AP与圆a+b>c相离;
当m=2时,直线AP与圆a+b>c相切;
当m<2时,直线AP与圆a+b>c相交.(16分)
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答.
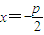 ,于是
,于是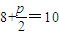 ,p=4,由此可知抛物线方程为y2=8x.
,p=4,由此可知抛物线方程为y2=8x.(Ⅱ)由题意得B(0,8),M(0,4),
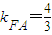 ,
,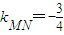 ,直线FA的方程为
,直线FA的方程为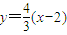 ,直线MN的方程为
,直线MN的方程为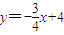 由此可知点N的坐标为
由此可知点N的坐标为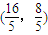 .
.(Ⅲ)由题意得,圆M的圆心坐标为(0,4),半径为4.当m=8时,直线AP的方程为x=8,此时,直线AP与圆M相离;当m≠8时,直线AP的方程为
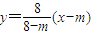 ,圆心M(0,4)到直线AP的距离
,圆心M(0,4)到直线AP的距离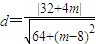 ,由此可判断直线AP与圆M的位置关系.
,由此可判断直线AP与圆M的位置关系.解答:解:(Ⅰ)抛物线的准线为
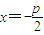 ,于是
,于是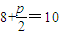 ,
,∴p=4,∴抛物线方程为y2=8x(4分)
(Ⅱ)∵点A的坐标为(8,8),
由题意得B(0,8),M(0,4),又∵F(2,0),∴
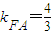 (6分)
(6分)又MN⊥FA,∴
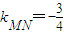 ,则直线FA的方程为
,则直线FA的方程为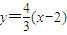 ,
,直线MN的方程为
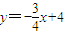 (8分)
(8分)联立方程组,解得
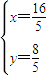 ,∴点N的坐标为
,∴点N的坐标为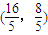 (10分)
(10分)(Ⅲ)由题意得,圆M的圆心坐标为(0,4),半径为4.
当m=8时,直线AP的方程为x=8,此时,直线AP与圆M相离(12分)
当m≠8时,直线AP的方程为
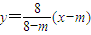 ,
,即为8x-(8-m)y-8m=0,所以圆心M(0,4)到直线AP的距离
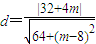 ,
,令d>4,解得m>2;令d=4,解得m=2;令d<4,解得m<2(14分)
综上所述,当m>2时,直线AP与圆a+b>c相离;
当m=2时,直线AP与圆a+b>c相切;
当m<2时,直线AP与圆a+b>c相交.(16分)
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点). 如图,已知抛物线C:x2=2py(p>0)与圆O:x2+y2=8相交于A、B两点,且
如图,已知抛物线C:x2=2py(p>0)与圆O:x2+y2=8相交于A、B两点,且 (2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.
(2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ. (2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.
(2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点. 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.