Question

如图，已知抛物线C：x²=2py（p＞0）与圆O：x²+y²=8相交于A、B两点，且

OA

•

OB

=0（O为坐标原点），直线l与圆O相切，切点在劣弧AB（含A、B两点）上，且与抛物线C相交于M、N两点，d是M、N两点到抛物线C的焦点的距离之和．
（Ⅰ）求p的值；
（Ⅱ）求d的最大值，并求d取得最大值时直线l的方程．

Answer 1

分析：（Ⅰ）设A（x₁，y₁）（x₁＜0），由抛物线C和圆O关于y轴对称，知点B的坐标为（-x₁，y₁）．由

OA

•

OB

=0，知-x₁²+y₁²=0．由点A在抛物线C上，知x₁²=2py₁．由此能求出p．
（Ⅱ） 解法1：设直线l的方程为：y=kx+b，由l是圆O的切线，知

|k•0-0+b|

k2+1

=2

2

，得到l的方程为：y=kx+2

2k2+2

．联立

y=kx+2 2k2+2 x2=2y.

，能求出直线l的方程．
解法2：设直线l与圆O相切的切点坐标为（x₀，y₀），则切线l的方程为x₀x+y₀y=8．由

x0x+y0y=8 x2=2y

，得y₀²y²-（16y₀+2x₀²）y+64=0．设M（x_M，y_M），N（x_N，y_N），则yM+yN=

16y0+2 x 2 0

y 2 0

．由此能求出直线l的方程．

解答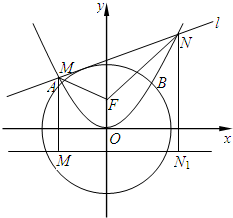：解：（Ⅰ）设点A的坐标为（x₁，y₁）（x₁＜0），
由于抛物线C和圆O关于y轴对称，故点B的坐标为（-x₁，y₁）．
∵

OA

•

OB

=0，
∴x₁•（-x₁）+y₁²=0，
即-x₁²+y₁²=0．
∵点A在抛物线C上，
∴x₁²=2py₁．
∴-2py₁+y₁²=0，即y₁（-2p+y₁）=0．
∵y₁≠0，
∴y₁=2p．
∴x₁=-2p．
∴点A的坐标为（-2p，2p）．
∵点A在圆O上，
∴（-2p）²+（2p）²=8，又p＞0，解得p=1．
（Ⅱ） 解法1：设直线l的方程为：y=kx+b，因为l是圆O的切线，则有

|k•0-0+b|

k2+1

=2

2

，
又b＞0，则b=2

2k2+2

．
即l的方程为：y=kx+2

2k2+2

．
联立

y=kx+2 2k2+2 x2=2y.

即y2-(2k2+4

2k2+2

)y+8(k2+1)=0．
设M（x_M，y_M），N（x_N，y_N），则yM+yN=2k2+4

2k2+2

．
如图，设抛物线C的焦点为F，准线为L，作MM₁⊥L，NN₁⊥L，垂足分别为M₁，N₁．
由抛物线的定义有：d=|MF|+|NF|=|MM₁|+|NN₁|=y_M+y_N+1=2k2+4

2k2+2

+1．
令t=

2k2+2

，则2k²=t²-2．
∴d=t²+4t-1=（t+2）²-5．
又∵-1≤k≤1，
∴

2

≤t≤2．
∴当t=2时，d有最大值11．
当t=2时，k=±1，故直线l的方程为y=±x+4．
解法2：设直线l与圆O相切的切点坐标为（x₀，y₀），则切线l的方程为x₀x+y₀y=8．
由

x0x+y0y=8 x2=2y

消去x，得y₀²y²-（16y₀+2x₀²）y+64=0．
设M（x_M，y_M），N（x_N，y_N），则yM+yN=

16y0+2 x 2 0

y 2 0

．
如图，设抛物线C的焦点为F，准线为L，作MM₁⊥L，NN₁⊥L，垂足分别为M₁，N₁．
由抛物线的定义有：d=|MF|+|NF|=|MM₁|+|NN₁|=y_M+y_N+1=

16y0+2 x 2 0

y 2 0

+1．
∵x₀²=8-y₀²，d=

16y0+2(8- y 2 0 )

y 2 0

+1=

16

y 2 0

+

16

y0

-1=16(

1

y0

+

1

2

)2-5．
∵2≤y0≤2

2

，
∴当y₀=2时，d有最大值11．
当y₀=2时，x₀=±2，故直线l的方程为y=±x+4．

点评：本题主要考查圆锥曲线标准方程，简单几何性质，直线与圆锥曲线的位置关系，圆锥曲线的简单性质等基础知识．考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想．