题目内容
如果双曲线x2-my2=1(m<1)上一点P与两焦点F1,F2构成的三角形面积为1,则此三角形的形状为
- A.直角三角形
- B.锐角三角形
- C.钝角三角形
- D.等边三角形
C
分析:先根据双曲线方程确定几何量,再利用三角形的面积公式及余弦定理,可建立方程,利用同角三角函数的平方关系,可用m表示cosα,利用m<1,即可求解.
解答:双曲线x2-my2=1(m<1)中,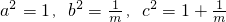
不妨设|PF2|=x,|PF1|=x+2,∠F1PF2=α
则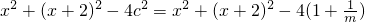 =2x(x+2)-
=2x(x+2)-
∵三角形的面积为1,
∴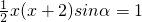
∴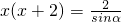
∵
∴
∵cos2α+sin2α=1
∴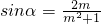
∴
∵m<1
∴cosα<0
∴α为钝角
故三角形为钝角三角形
故选C.
点评:本题以双曲线为载体,考查双曲线的焦点三角形,合理运用双曲线的定义,正确运用余弦定理是解题的关键.
分析:先根据双曲线方程确定几何量,再利用三角形的面积公式及余弦定理,可建立方程,利用同角三角函数的平方关系,可用m表示cosα,利用m<1,即可求解.
解答:双曲线x2-my2=1(m<1)中,
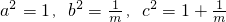
不妨设|PF2|=x,|PF1|=x+2,∠F1PF2=α
则
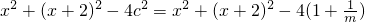 =2x(x+2)-
=2x(x+2)-
∵三角形的面积为1,
∴
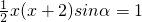
∴
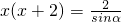
∵

∴

∵cos2α+sin2α=1
∴
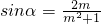
∴

∵m<1
∴cosα<0
∴α为钝角
故三角形为钝角三角形
故选C.
点评:本题以双曲线为载体,考查双曲线的焦点三角形,合理运用双曲线的定义,正确运用余弦定理是解题的关键.

练习册系列答案
相关题目
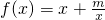 ,且此函数图象过点(1,5).
,且此函数图象过点(1,5).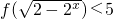 .
.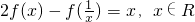 且x≠0.
且x≠0. (a>0,b>0)的右焦点为F,若过点F且斜率为
(a>0,b>0)的右焦点为F,若过点F且斜率为 的直线与双曲线渐近线平行,则此双曲线离心率是
的直线与双曲线渐近线平行,则此双曲线离心率是
