题目内容
已知常数![]() 、
、![]() 都是实数,在数列
都是实数,在数列![]() 与
与![]() 中
中![]() .对任何正整数
.对任何正整数![]() ,等式
,等式![]() ,
,![]() 都成立。
都成立。
(Ⅰ)当![]() 时,求数列
时,求数列![]() 与
与![]() 的通项公式;
的通项公式;
(Ⅱ)当![]() 且
且![]() 时,要使数列
时,要使数列![]() 是公比不为1等比数列,求
是公比不为1等比数列,求![]() 的值;
的值;
(Ⅲ)当![]() 时,设数列
时,设数列![]() 的前
的前![]() 项和、
项和、![]() 的前
的前![]() 项和分别为
项和分别为![]() 与
与![]() ,
,
求![]() 的值.
的值.
解:(Ⅰ)![]() .
.
![]()
![]() 、
、![]() 都是公差为
都是公差为![]() 的等差数列.
的等差数列.
![]() ,
,![]() ,
,![]() .
.
(Ⅱ)![]()
![]() 是等比数列,
是等比数列,![]() 为常数。
为常数。![]() 是公比不为1的等比数列,
是公比不为1的等比数列,
![]() 不是常数,
不是常数,![]() 必有
必有![]()
(Ⅲ)解:![]() ,
,![]() ,
, ![]() .
.
两式相减得:![]() 为等比数列,
为等比数列,
![]() .
.
![]() …
…![]() …
…![]() .
.
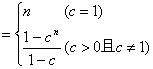 .
.
∴当![]() 时,
时,![]() …
…![]() …
…![]() .
.
=![]() …
…![]() .
.
=![]() ,
,
∴当![]() 且
且![]() 时,
时,![]() …
…![]() …
…![]() .
.
=![]() …
…![]() .
.
=![]() …
…![]() .
.
=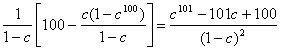 .
.

练习册系列答案
相关题目
 的导函数为f′(x)
的导函数为f′(x) 、
、 、
、 都是实数,函数
都是实数,函数 的导函数为
的导函数为 ,
, 的解集为
的解集为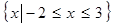 .
. 的极大值等于
的极大值等于 ,求
,求 的解集为集合
的解集为集合 ,当
,当 时,函数
时,函数 只有一个零点,求实数
只有一个零点,求实数 的取值范围.
的取值范围.