题目内容
定义域为R的函数 满足条件:
满足条件:
① ;
;
②
 ; ③
; ③ .
.
则不等式 的解集是( )
的解集是( )
A. | B. |
C. | D. |
D
解析试题分析:根据题意可知 ,函数是一个奇函数,同时
,函数是一个奇函数,同时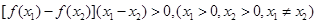 ,结合单调性定义可知为单调增函数,在x>0时,同时f(-3)=-f(3)=0,那么结合函数的性质可知,
,结合单调性定义可知为单调增函数,在x>0时,同时f(-3)=-f(3)=0,那么结合函数的性质可知, 的解集为
的解集为 ,选D.
,选D.
考点:本题主要是考查不等式的解集和函数奇偶性的运用。
点评:解决该试题的关键是理解抽象函数的性质和作出草图,然后得到结论,同时要对于x分情况讨论。

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
下列四组函数中,表示相同函数的一组是( )
A. | B. |
C. | D. |
已知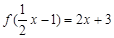 ,
, 则
则 等于 ( )
等于 ( )
A.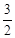 | B.  | C. | D. |
已知函数 为奇函数,则
为奇函数,则 的值为( )
的值为( )
A. | B. | C. | D. |
若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为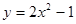 ,值域为
,值域为 的“孪生函数”共有( )
的“孪生函数”共有( )
| A.10个 | B.9个 | C.8个 | D.4个 |
若关于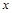 的方程
的方程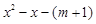 =0在
=0在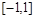 上有解,则
上有解,则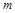 的取值范围是 ( )
的取值范围是 ( )
A.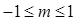 | B.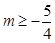 | C. | D.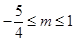 |
对于实数 ,符号
,符号 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,定义函数
,定义函数 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A. | B.方程 有且仅有一个解 有且仅有一个解 |
C.函数 是周期函数 是周期函数 | D.函数 是增函数 是增函数 |
下列函数中,值域为(0, )的函数是( )
)的函数是( )
A. | B. | C. | D. |
 的图像是( )
的图像是( )
