题目内容
已知定义在R的函数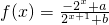 (a,b为实常数).
(a,b为实常数).
(Ⅰ)当a=b=1时,证明:f(x)不是奇函数;
(Ⅱ)设f(x)是奇函数,求a与b的值;
(Ⅲ)当f(x)是奇函数时,证明对任何实数x、c都有f(x)<c2-3c+3成立.
解:(Ⅰ)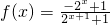 ,
,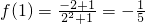 ,
,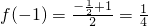 ,
,
所以f(-1)≠-f(1),f(x)不是奇函数;(2分)
(Ⅱ)f(x)是奇函数时,f(-x)=-f(x),
即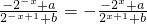 对任意x∈R恒成立.(4分)
对任意x∈R恒成立.(4分)
化简整理得(2a-b)•22x+(2ab-4)•2x+(2a-b)=0对任意x∈R恒成立.(6分)
∴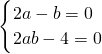 ,∴
,∴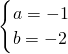 (舍)或
(舍)或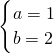 ,∴
,∴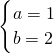 .(8分)
.(8分)
另解:∵f(x)是定义在R的奇函数,∴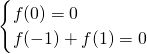 ,,
,,
∴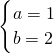 ,验证满足,∴
,验证满足,∴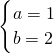 .
.
(Ⅲ)由(Ⅱ)得: ,
,
∵2x>0,∴2x+1>1,
∴ ,从而
,从而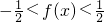 ;(12分)
;(12分)
而 对任何实数c成立;
对任何实数c成立;
所以对任何实数x、c都有f(x)<c2-3c+3成立.(14分)
分析:(I)证明不是奇函数,可用特殊值法;
(II)用奇函数定义f(-x)=-f(x),再用待定系数法求解;
(III)即证明c2-3c+3大于f(x)的最大值,所以先求f(x)的最大值.
点评:本题主要考查奇函数的应用及恒成立问题.
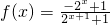 ,
,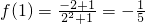 ,
,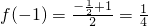 ,
,所以f(-1)≠-f(1),f(x)不是奇函数;(2分)
(Ⅱ)f(x)是奇函数时,f(-x)=-f(x),
即
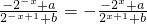 对任意x∈R恒成立.(4分)
对任意x∈R恒成立.(4分)化简整理得(2a-b)•22x+(2ab-4)•2x+(2a-b)=0对任意x∈R恒成立.(6分)
∴
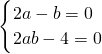 ,∴
,∴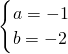 (舍)或
(舍)或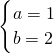 ,∴
,∴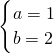 .(8分)
.(8分)另解:∵f(x)是定义在R的奇函数,∴
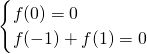 ,,
,,∴
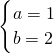 ,验证满足,∴
,验证满足,∴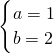 .
.(Ⅲ)由(Ⅱ)得:
 ,
,∵2x>0,∴2x+1>1,
∴
 ,从而
,从而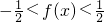 ;(12分)
;(12分)而
 对任何实数c成立;
对任何实数c成立;所以对任何实数x、c都有f(x)<c2-3c+3成立.(14分)
分析:(I)证明不是奇函数,可用特殊值法;
(II)用奇函数定义f(-x)=-f(x),再用待定系数法求解;
(III)即证明c2-3c+3大于f(x)的最大值,所以先求f(x)的最大值.
点评:本题主要考查奇函数的应用及恒成立问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知定义在R的函数f(x)=m+
为奇函数,则m的值是( )
| 1 |
| 2x+1 |
| A、0 | ||
B、-
| ||
C、
| ||
| D、2 |
 (a,b为实常数).
(a,b为实常数).