题目内容
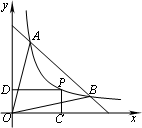
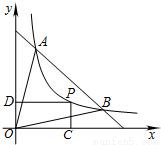
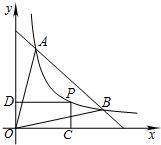 如图,反比例函数y=f(x)(x>0)的图象过点A(1,4)和B(4,1),点P(x,y)为该函数图象上一动点,过P分别作x轴、y轴的垂线,垂足为C、D.记四边形OCPD(O为坐标原点)与三角形OAB的公共部分面积为S.
如图,反比例函数y=f(x)(x>0)的图象过点A(1,4)和B(4,1),点P(x,y)为该函数图象上一动点,过P分别作x轴、y轴的垂线,垂足为C、D.记四边形OCPD(O为坐标原点)与三角形OAB的公共部分面积为S.(1)求S关于x的表达式;
(2)求S的最大值及此时x的值.
分析:(1)根据图象求得反比例函数模型,由题设,得f(x)=
(x>0),再分x≤1时,1<x<4时,x≥4时三种情况求得其面积建立模型.
(2)根据(1)函数是分段函数每一段根据函数的特点取得取大值,然后从中取最大的,作为原函数的最大值.
| 4 |
| x |
(2)根据(1)函数是分段函数每一段根据函数的特点取得取大值,然后从中取最大的,作为原函数的最大值.
解答:解:(1)由题设,得f(x)=
(x>0),(2分)
当x≤1时,S=
x2,
当1<x<4时,S=4-
-
,
当x≥4时,S=
,
故S=
(8分)
(2)易知当x≤1时,S=
x2为单调递增函数,S≤
,(10分)
当x≥4时,S=
为单调递减函数,S≤
,(12分)
当1<x<4时,S=4-
-
在区间(1,2)上单调递增,在区间(2,4)上单调递减,得
<S≤3,
故S的最大值为3,
此时x=2.(16分)
| 4 |
| x |
当x≤1时,S=
| 15 |
| 8 |
当1<x<4时,S=4-
| x2 |
| 8 |
| 2 |
| x2 |
当x≥4时,S=
| 30 |
| x2 |
故S=
|
(2)易知当x≤1时,S=
| 15 |
| 8 |
| 15 |
| 8 |
当x≥4时,S=
| 30 |
| x2 |
| 15 |
| 8 |
当1<x<4时,S=4-
| x2 |
| 8 |
| 2 |
| x2 |
| 15 |
| 8 |
故S的最大值为3,
此时x=2.(16分)
点评:本题主要考查函数模型的建立与应用,主要涉及了分段函数求最值,基本思想是求每一段上取最大值,从中取最大的作为原函数的最大值.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
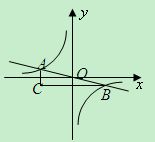 如图,反比例函数
如图,反比例函数