题目内容
2.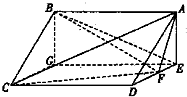 如图,在三棱柱BCG-ADE中,四边形ABCD为正方形,AE⊥平面CDE,AE=DE=2,FD=EF.
如图,在三棱柱BCG-ADE中,四边形ABCD为正方形,AE⊥平面CDE,AE=DE=2,FD=EF.(Ⅰ)求证:BE∥平面ACF;
(Ⅱ)求二面角B-CF-A的平面角的余弦值.
分析 (Ⅰ)根据线面平行的判定定理即可证明BE∥平面ACF;
(Ⅱ)建立空间直角坐标系,求出平面的法向量,利用向量法即可求二面角B-CF-A的平面角的余弦值.
解答 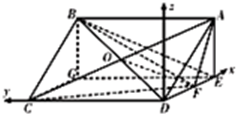 证明:(Ⅰ)连接BD和AC交于O,连接OF,
证明:(Ⅰ)连接BD和AC交于O,连接OF,
∵O为BD的中点,F是DE的中点,
∴OF∥BE,
∵BE?平面ACF,CD?平面ACF;
∴BE∥平面ACF;
(Ⅱ)∵AE⊥平面CDE,CD?平面ACF,
∴AE⊥CD,
∵四边形ABCD为正方形,
∴CD⊥AD,
∵AE∩AD=A,AD,AE?平面DAE;
∴CD⊥平面DAE,
∵DE?平面DAE,
∴CD⊥DE,
故以D为原点,以DE为x轴,建立如图所示的坐标系,
则E(2,0,0),F(1,0,0),A(2,0,2),D(0,0,0),
由AE=DE=2,得AD=2$\sqrt{2}$,CD=2$\sqrt{2}$,
故C(0,2$\sqrt{2}$,0),
由$\overrightarrow{DB}=\overrightarrow{DA}+\overrightarrow{DC}$=(2,2$\sqrt{2}$,2),
故B(2,2$\sqrt{2}$,2).
设平面ACF的法向量为$\overrightarrow{m}$=(x,y,z),
$\overrightarrow{AC}$=(-2,2$\sqrt{2}$,-2),$\overrightarrow{CF}$=(1,-2$\sqrt{2}$,0),
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AC}=0}\\{\overrightarrow{m}•\overrightarrow{CF}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-2x+2\sqrt{2}y-2z=0}\\{x-2\sqrt{2}y=0}\end{array}\right.$,
令y=1,则x=2$\sqrt{2}$,z=-$\sqrt{2}$,
即$\overrightarrow{m}$=(2$\sqrt{2}$,1,-$\sqrt{2}$),
设平面BCF的法向量为$\overrightarrow{n}$=(x,y,z),
$\overrightarrow{BC}$=(-2,0,-2),$\overrightarrow{CF}$=(1,-2$\sqrt{2}$,0),
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BC}=0}\\{\overrightarrow{n}•\overrightarrow{CF}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-2x-2z=0}\\{x-2\sqrt{2}y=0}\end{array}\right.$,
令y=1,则x=2$\sqrt{2}$,z=-2$\sqrt{2}$,
即$\overrightarrow{n}$=(2$\sqrt{2}$,1,-2$\sqrt{2}$),
cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{8+1+4}{\sqrt{11}×\sqrt{17}}$=$\frac{13\sqrt{187}}{187}$
即二面角B-CF-A的平面角的余弦值为$\frac{13\sqrt{187}}{187}$.
点评 本题主要考查线面平行的判定,以及二面角的求解,建立空间坐标系,利用向量法是解决二面角的常用方法.考查学生的运算和推理能力.

| A. | (0,+∞) | B. | (-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$) | C. | (-$∞,-\frac{\sqrt{3}}{2}$) | D. | (-∞,0) |
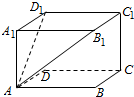 如图,长方体ABCD-A1B1C1D1中,AA1=$\sqrt{3}$,AD1=$\sqrt{5}$,AB1=$\sqrt{7}$,则长方体的对角线AC1长等于3.
如图,长方体ABCD-A1B1C1D1中,AA1=$\sqrt{3}$,AD1=$\sqrt{5}$,AB1=$\sqrt{7}$,则长方体的对角线AC1长等于3. 已知点A,B,C都在以原点O为圆心点的圆上,其中$\overrightarrow{OA}$=(-3,4),点B位于第一象限,点C为圆O与x轴正半轴的交点,若△BOC为正三角形.
已知点A,B,C都在以原点O为圆心点的圆上,其中$\overrightarrow{OA}$=(-3,4),点B位于第一象限,点C为圆O与x轴正半轴的交点,若△BOC为正三角形.