题目内容
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明).
的通项公式(不必证明).
(2)将数列![]() 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值.
的值.
(3)设![]() 为数列
为数列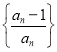 的前
的前![]() 项积,且
项积,且![]() ,求数列
,求数列![]() 的最大项.
的最大项.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)2010;(3)
;(2)2010;(3)![]() .
.
【解析】
(1)化简得到![]() ,计算
,计算![]() ,
,![]() ,
,![]() ,猜想
,猜想![]() 得到答案.
得到答案.
(2)计算![]() ,再计算
,再计算![]() ,相加得到答案.
,相加得到答案.
(3)计算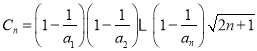 ,故
,故![]() ,故
,故![]() 是单调递减,计算
是单调递减,计算![]() 得到答案.
得到答案.
(1)因为点![]() 在函数
在函数![]() 的图象上,故
的图象上,故![]() ,所以
,所以![]() .令
.令![]() ,得
,得![]() ,所以
,所以![]() ;
;
令![]() ,得
,得![]() ,所以
,所以![]() ;
;
令![]() ,得
,得![]() ,所以
,所以![]() ;
;
由此猜想:![]() .
.
(2)因为![]() ,所以数列
,所以数列![]() 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,
每一次循环记为一组.由于每一个循环含有4个括号,
故![]() 是第25组中第4个括号内各数之和.
是第25组中第4个括号内各数之和.
由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20.
同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20.
故各组第4个括号中各数之和构成等差数列,且公差为80.
注意到第一组中第4个括号内各数之和是68,所以![]() .
.
又![]() ,所以
,所以![]() .
.
(3)因为![]() ,故
,故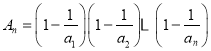 ,
,
所以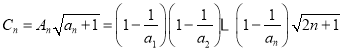 .
.
由于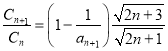
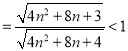 ,
,
所以![]() ,故
,故![]() 是单调递减,
是单调递减,
于是数列![]() 的最大项为
的最大项为![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目