题目内容
如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
箱子底边长取40 cm时,容积最大,最大容积为16 000 cm3.
解析试题分析:设箱子的底边长为x cm,则箱子高h=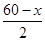 cm.
cm.
箱子容积V=V(x)=x2h=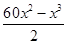 (0<x<60).
(0<x<60).
求V(x)的导数,得V′(x)=60x-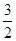 x2=0,
x2=0,
解得x1=0(不合题意,舍去),x2=40.
当x在(0,60)内变化时,导数V′(x)的正负如下表:
因此在x=40处,函数V(x)取得极大值,并且这个极大值就是函数V(x)的最大值.x (0,40) 40 (40,60) V′(x) + 0 -
将x=40代入V(x)
得最大容积V=402×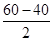 =16 000(cm3).
=16 000(cm3).
所以箱子底边长取40 cm时,容积最大,最大容积为16 000 cm3.
考点:本题主要考查函数模型,应用导数研究函数的单调性、最值。
点评:典型题,本题属于函数及导数应用中的基本问题,通过研究构建函数函数模型,利用导数求函数的最值。关于函数应用问题的考查,在高考题中往往是“一大两小”。构建函数模型的步骤“审清题意、设出变量、确定函数、求解答案、写出结语”。本题利用均值定理,确定函数的最值。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
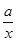 (x≠0).
(x≠0).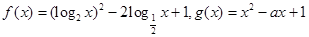
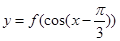 的定义域;
的定义域;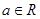 ,对任意
,对任意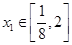 ,总存在唯一
,总存在唯一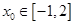 ,使得
,使得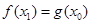 成立.求实数
成立.求实数 的取值范围.
的取值范围.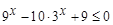 ,求函数
,求函数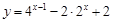 的最大值和最小值;
的最大值和最小值; 在
在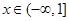 上f (x)
上f (x)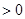 恒成立,求a的取值范围.
恒成立,求a的取值范围.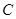 (单位:万元)与日产量
(单位:万元)与日产量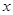 (单位:吨)满足函数关系式
(单位:吨)满足函数关系式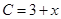 ,每日的销售额
,每日的销售额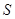 (单位:万元)与日产量
(单位:万元)与日产量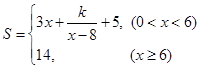
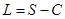 ,且当
,且当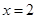 时,
时,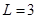 .
.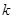 的值;
的值;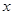 (件)之间近似满足关系:
(件)之间近似满足关系: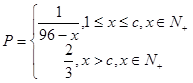 (其中
(其中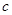 为小于96的正整常数)
为小于96的正整常数) ,如P=0.1表示每生产10件产品,有1件次品,其余为合格品.)已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损A/2元,故厂方希望定出合适的日产量。
,如P=0.1表示每生产10件产品,有1件次品,其余为合格品.)已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损A/2元,故厂方希望定出合适的日产量。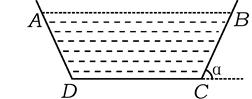
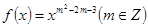 为偶函数,且在区间
为偶函数,且在区间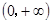 上是单调减函数(Ⅰ)求函数
上是单调减函数(Ⅰ)求函数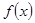 ;(Ⅱ)讨论
;(Ⅱ)讨论 的奇偶性.
的奇偶性.