题目内容
已知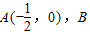
是圆
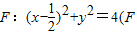为圆心）上一动点，线段AB的垂直平分线交BF于P，则动点P的轨迹方程为 ．
【答案】分析：先根据题意可知|BP|+|PF|正好为圆的半径，而PB|=|PA|，进而可知|AP|+|PF|=2．根据椭圆的定义可知，点P的轨迹为以A，F为焦点的椭圆，根据A，F求得a，c，进而求得b，答案可得．
解答：解：依题意可知|BP|+|PF|=2，|PB|=|PA|
∴|AP|+|PF|=2
根据椭圆的定义可知，点P的轨迹为以A，F为焦点的椭圆，
a=1，c=
，则有b=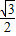
故点P的轨迹方程为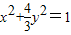
故答案为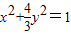
点评：本题主要考查了用定义法求轨迹方程的问题．考查了学生综合分析问题和解决问题的能力．
解答：解：依题意可知|BP|+|PF|=2，|PB|=|PA|
∴|AP|+|PF|=2
根据椭圆的定义可知，点P的轨迹为以A，F为焦点的椭圆，
a=1，c=
，则有b=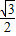故点P的轨迹方程为
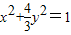
故答案为
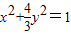
点评：本题主要考查了用定义法求轨迹方程的问题．考查了学生综合分析问题和解决问题的能力．
练习册系列答案
相关题目
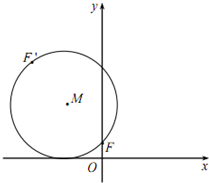（2012•深圳二模）如图，已知动圆M过定点F（0，1）且与x轴相切，点F关于圆心M的对称点为F′，动点F′的轨迹为C．
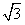c，0)三点，其中c＞0，
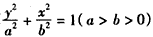（其中a2-b2=c2）的左、右顶点分别为D，B，圆M与x轴的两个交点分别为A，C，且A点在B点右侧，C点在D点右侧，