题目内容
有下述命题
①若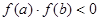 ,则函数
,则函数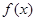 在
在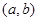 内必有零点;
内必有零点;
②当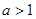 时,总存在
时,总存在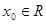 ,当
,当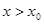 时,总有
时,总有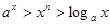 ;
;
③函数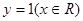 是幂函数;
是幂函数;
④若
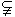
 ,则
,则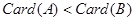 其中真命题的个数是( )
其中真命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
B
解析试题分析:①若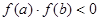 ,则函数
,则函数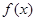 在
在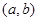 内必有零点,若函数
内必有零点,若函数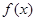 在
在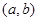 内不连续,就没有零点,故为命题假;②当
内不连续,就没有零点,故为命题假;②当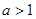 时,总存在
时,总存在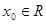 ,当
,当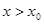 时,总有
时,总有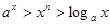 ,在区间
,在区间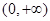 上,尽管指数函数
上,尽管指数函数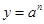 (
( >1),幂函数
>1),幂函数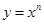 (
(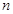 >0),对数函数
>0),对数函数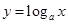 (
( >1)在区间
>1)在区间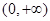 上都是增函数,但它们的增长速度不同,而且不在同一个‘档次’上,随着
上都是增函数,但它们的增长速度不同,而且不在同一个‘档次’上,随着 的增大,指数函数
的增大,指数函数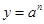 的增长速度越来越快,会超过并远远大于幂函数
的增长速度越来越快,会超过并远远大于幂函数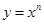 的增长速度,而对数函数
的增长速度,而对数函数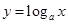 (
( >1)的增长速度则会越来越慢.因此,总会存在一个
>1)的增长速度则会越来越慢.因此,总会存在一个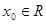 ,当
,当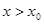 时,就有
时,就有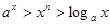 ;故为真命题,③函数
;故为真命题,③函数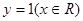 是幂函数,不是幂函数,它是常数函数,故为命题假;④若
是幂函数,不是幂函数,它是常数函数,故为命题假;④若
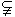
 ,则
,则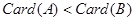 ,当
,当 ,
, 都是无限集时,就不成立,故为命题假.
都是无限集时,就不成立,故为命题假.
考点:命题的真假判断与应用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
命题甲:双曲线C的方程为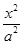 -
-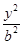 =1(其中
=1(其中 ;命题乙:双曲线C的渐近线方程为y=±
;命题乙:双曲线C的渐近线方程为y=±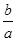 x;那么甲是乙的( )
x;那么甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若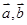 为平面向量,则“
为平面向量,则“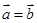 ”是“
”是“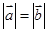 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
在△ABC中,“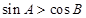 ”是“△ABC是锐角三角形”的( )
”是“△ABC是锐角三角形”的( )
| A.充分必要条件 | B.充分而不必要条件 |
| C.必要而不充分条件 | D.既不充分又不必要条件 |
 是
是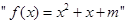 有零点的( )
有零点的( )
| A.充分不必要条件 | B.充要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
命题“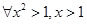 ” 的否定是( )
” 的否定是( )
A.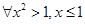 | B. |
C.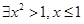 | D.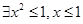 |
“数列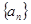 为常数列”是“数列
为常数列”是“数列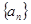 既是等差数列又是等比数列”的( )
既是等差数列又是等比数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给出命题:已知 为实数,若
为实数,若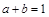 ,则
,则 .在它的逆命题、否命题、逆否命三个命题中,假命题的个数是( )
.在它的逆命题、否命题、逆否命三个命题中,假命题的个数是( )
| A.3 | B.2 | C.1 | D.0 |
4. 下列命题中的假命题是( )
A.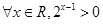 | B.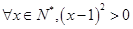 |
C.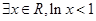 | D.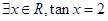 |