题目内容
函数y=f(x)定义在R上单调递减且f(0)≠0,对任意实数m、n,恒有f(m+n)=f(m)•f(n),集合A={(x,y)|f(x2)•f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=φ,则a的取值范围是 .
【答案】分析:利用f(m+n)=f(m)•f(n)及y=f(x)为单调递减函数,化简集合A,得到确定出集合A中元素为圆心是原点,半径为1的单位圆内的点组成的集合;令m=n=0,代入f(m+n)=f(m)•f(n),根据f(0)≠0,得到f(0)的值,进而根据f(x)单调,把集合B中的1变为f(0),进而确定出集合B为直线ax-y+2=0上点组成的集合,根据题意画出函数图象,先求出直线与圆相切时的a的值,根据图象写出满足题意的a的范围即可.
解答:解:由集合A中的不等式f(x2)•f(y2)>f(1),
变形为:f(x2)•f(y2)=f(x2+y2)>f(1),
又函数y=f(x)定义在R上单调递减,得到x2+y2<1,
即集合A是圆心为(0,0),半径为1的圆内的所有的点所构成的集合;
令m=0,n=0,得到f(0+0)=f(0)•f(0),即f(0)[f(0)-1]=0,又f(0)≠0,
所以f(0)=1,则集合B中的等式f(ax-y+2)=1=f(0),由函数y=f(x)单调,
得到ax-y+2=0,即集合B是直线ax-y+2=0上的点的坐标构成的集合,
根据题意画出图象,如图所示:
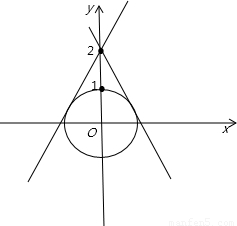
由A∩B=∅,所以圆与直线没有交点,特殊情况为直线ax-y+2=0与圆x2+y2=0相切,
圆心到直线的距离d=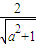 =1,解得a=
=1,解得a=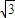 或-
或-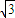 ,
,
则满足题意的a的取值范围是:-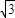 ≤a≤
≤a≤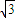 .
.
故答案为:-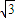 ≤a≤
≤a≤
点评:此题考查学生掌握直线与圆的位置关系,灵活运用点到直线的距离公式化简求值,考查了数形结合的思想,是一道中档题.
解答:解:由集合A中的不等式f(x2)•f(y2)>f(1),
变形为:f(x2)•f(y2)=f(x2+y2)>f(1),
又函数y=f(x)定义在R上单调递减,得到x2+y2<1,
即集合A是圆心为(0,0),半径为1的圆内的所有的点所构成的集合;
令m=0,n=0,得到f(0+0)=f(0)•f(0),即f(0)[f(0)-1]=0,又f(0)≠0,
所以f(0)=1,则集合B中的等式f(ax-y+2)=1=f(0),由函数y=f(x)单调,
得到ax-y+2=0,即集合B是直线ax-y+2=0上的点的坐标构成的集合,
根据题意画出图象,如图所示:

由A∩B=∅,所以圆与直线没有交点,特殊情况为直线ax-y+2=0与圆x2+y2=0相切,
圆心到直线的距离d=
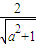 =1,解得a=
=1,解得a=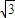 或-
或-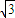 ,
,则满足题意的a的取值范围是:-
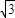 ≤a≤
≤a≤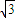 .
.故答案为:-
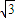 ≤a≤
≤a≤
点评:此题考查学生掌握直线与圆的位置关系,灵活运用点到直线的距离公式化简求值,考查了数形结合的思想,是一道中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目