题目内容
已知动圆M与直线y=2相切,且与定圆C:x2+(y+3)2=1外切,动圆圆心M的轨迹方程是
x2=-12y
x2=-12y
.分析:根据动圆M与直线y=2相切,且与定圆C:x2+(y+3)2=1外切,可得动点M到C(0,-3)的距离与到直线y=3的距离相等,由抛物线的定义知,点M的轨迹是抛物线,由此易得轨迹方程.
解答:解:由题意动圆M与直线y=2相切,且与定圆C:x2+(y+3)2=1外切
∴动点M到C(0,-3)的距离与到直线y=3的距离相等
由抛物线的定义知,点M的轨迹是以C(0,-3)为焦点,直线y=3为准线的抛物线
故所求M的轨迹方程为:x2=-12y.
故答案为:x2=-12y.
∴动点M到C(0,-3)的距离与到直线y=3的距离相等
由抛物线的定义知,点M的轨迹是以C(0,-3)为焦点,直线y=3为准线的抛物线
故所求M的轨迹方程为:x2=-12y.
故答案为:x2=-12y.
点评:本题考查轨迹方程,熟记抛物线的定义是求解本题的关键,考查转化思想与计算能力.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
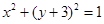 外切,求动圆圆心M的轨迹方程.
外切,求动圆圆心M的轨迹方程.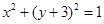 外切,求动圆圆心M的轨迹方程.(12分)
外切,求动圆圆心M的轨迹方程.(12分)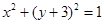 外切,求动圆圆心M的轨迹方程.(12分)
外切,求动圆圆心M的轨迹方程.(12分)