题目内容
已知动圆M与直线y =2相切，且与定圆C：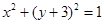
外切，求动圆圆心M的轨迹方程．(12分)
【答案】
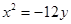
【解析】主要考查抛物线定义、标准方程、几何性质。
解：设动圆圆心为M（x，y），半径为r，则由题意可得M到C（0，-3）的距离与到直线y=3的距离相等，由抛物线的定义可知：动圆圆心的轨迹是以C（0，-3）为焦点，以y=3为准线的一条抛物线，其方程为．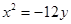
练习册系列答案
中考解读考点精练系列答案
相关题目
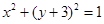外切，求动圆圆心M的轨迹方程．
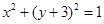外切，求动圆圆心M的轨迹方程．(12分)