题目内容
1.满足约束条件$\left\{\begin{array}{l}{x-3z≤0}\\{x-y+6z≥0}\\{x+y≥0}\\{x,y>0,z>0}\end{array}\right.$,则$\frac{y+3z}{x}$的取值范围是(1,+∞).分析 设令a=$\frac{y}{x}$,b=$\frac{3z}{x}$,将不等式组进行转化,利用线性规划的知识进行求解即可.
解答 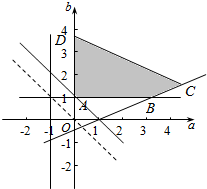 解:不等式等价为$\left\{\begin{array}{l}{1-\frac{3z}{x}≤0}\\{1-\frac{y}{x}+\frac{6z}{x}≥0}\\{1+\frac{y}{x}≥0}\end{array}\right.$,
解:不等式等价为$\left\{\begin{array}{l}{1-\frac{3z}{x}≤0}\\{1-\frac{y}{x}+\frac{6z}{x}≥0}\\{1+\frac{y}{x}≥0}\end{array}\right.$,
令a=$\frac{y}{x}$,b=$\frac{3z}{x}$,则a>0,b>0,
则不等式组等价为$\left\{\begin{array}{l}{1-b≤0}\\{1-a+2b≥0}\\{1+a≥0}\end{array}\right.$,
作出不等式组对应的平面区域如图:
则$\frac{y+3z}{x}$=$\frac{y}{x}$+$\frac{3z}{x}$=a+b,
设m=a+b,
则b=-a+m,
平移直线b=-a+m由图象知当直线b=-a+m经过点A(0,1)时,直线的截距最小,此时m最小,无最大值,
则m=0+1=1.
即m>1,
则$\frac{y+3z}{x}$的取值范围是(1,+∞),
故答案为:(1,+∞)
点评 本题主要考查线性规划的应用,根据条件利用换元法将三元不等式转化为二元不等式组是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知O是三角形ABC内部一点,满足$\overrightarrow{OA}$+2$\overrightarrow{OB}$=4$\overrightarrow{CO}$,则$\frac{{S}_{△AOB}}{{S}_{△AOC}}$=( )
| A. | $\frac{3}{2}$ | B. | 5 | C. | 2 | D. | $\frac{5}{3}$ |