题目内容
 如图,三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2
如图,三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2| 3 |
(Ⅰ)证明:AB⊥VC;
(Ⅱ)求三棱锥V-ABC的体积.
分析:(Ⅰ)通过证明直线AB⊥平面VDC,然后证明AB⊥VC;
(Ⅱ)求三棱锥V-ABC的体积.
(Ⅱ)求三棱锥V-ABC的体积.
解答: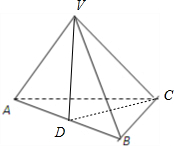 证明:(Ⅰ)取AB的中点为D,连接VD,CD.
证明:(Ⅰ)取AB的中点为D,连接VD,CD.
∵VA=VB,∴AB⊥VD;同理AB⊥CD.
于是AB⊥平面VDC.又VC?平面VDC,故AB⊥VC.
解:(Ⅱ)由(Ⅰ)知AB⊥平面VDC.
由题设可知VD=CD=1,又VC=1,DB=
.CD=VD=
=1,S△VDC=
×1×
,
故三棱锥V-ABC的体积等于
S△VDC•BA=
×(
×1×
)×2
=
.
 证明:(Ⅰ)取AB的中点为D,连接VD,CD.
证明:(Ⅰ)取AB的中点为D,连接VD,CD.∵VA=VB,∴AB⊥VD;同理AB⊥CD.
于是AB⊥平面VDC.又VC?平面VDC,故AB⊥VC.
解:(Ⅱ)由(Ⅰ)知AB⊥平面VDC.
由题设可知VD=CD=1,又VC=1,DB=
| 3 |
22-(
|
| 1 |
| 2 |
| ||
| 2 |
故三棱锥V-ABC的体积等于
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
点评:本题考查直线与平面的垂直的性质定理以及棱锥体积的求法,考查逻辑思维能力与计算能力.

练习册系列答案
相关题目
 15、如图,三棱锥V-ABC中,VA⊥底面ABC,∠ABC=90°.
15、如图,三棱锥V-ABC中,VA⊥底面ABC,∠ABC=90°. 如图,三棱锥V-ABC中,VA=VB=AC=BC=2,AB=
如图,三棱锥V-ABC中,VA=VB=AC=BC=2,AB= 如图,三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD,则下列结论中不一定成立的是( )
如图,三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD,则下列结论中不一定成立的是( ) 如图,三棱锥V-ABC中,AB=AC=VB=VC=
如图,三棱锥V-ABC中,AB=AC=VB=VC=