已知数列{an}的首项a1=1.an=an-1+3(n≥2.n∈N*).则a4=( )A．10B．11C．9D．8 题目和参考答案——青夏教育精英家教网——

题目内容

13．已知数列{a_n}的首项a₁=1，a_n=a_n-1+3（n≥2，n∈N^*），则a₄=（　　）

A．

10

B．

11

C．

9

D．

8

分析由题意可判数列为等差数列，由通项公式可得．

解答解：由a_n=a_n-1+3可得a_n-a_n-1=3，
∴数列{a_n}构成1为首项3为公差的等差数列，
∴a₄=a₁+3d=1+3×3=10
故选：A

点评本题考查等差数列的通项公式，属基础题．

练习册系列答案

Happy寒假作业快乐寒假系列答案

金象教育U计划学期系统复习寒假作业系列答案

八斗才火线计划寒假西安交通大学出版社系列答案

伴你成长橙色寒假系列答案

帮你学寒假作业系列答案

备战中考寒假系列答案

创新大课堂系列丛书寒假作业系列答案

创新自主学习寒假新天地系列答案

创优教学寒假作业年度总复习系列答案

导学练寒假作业云南教育出版社系列答案

相关题目

4．将两颗骰子各掷一次，设事件A=“两个点数不相同”，B=“至少出现一个6点”，则概率P（A|B）等于（　　）

$\frac{10}{11}$

4．已知ξ～N（1，4），若P（ξ＜2）=1-P（ξ＜a），则a=0．

1．已知函数y=a-bcos（2x+$\frac{π}{6}$）（b＞0）的最大值为$\frac{3}{2}$，最小值为-$\frac{1}{2}$，则实数a，b的值为?$\frac{1}{2}$，1．

8．（1）若将一粒骰子连续抛掷两次（骰子是有六个面的正方体且每个面分别标有1，2，3，4，5，6）所得到点数分别记为a、b．记“关于x的一元二次方程x²+2ax+b²=0有实根”为事件C．求事件C发生的概率；
（2）若a、b均为从区间[0，6]内任取的一个实数，记事件D表示“a²+b²≤16”，求事件D发生的概率．

18．数列{a_n}的通项公式为a_n=2n+1，b_n=$\frac{1}{{a}_{1}+{a}_{2}+…+{a}_{n}}$，则数列{b_n}的前n项和为$\frac{1}{2}$（$\frac{3}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$）．

5．已知函数f（x）=-$\sqrt{4+\frac{1}{{x}^{2}}}$，点P_n（a_n，-$\frac{1}{{a}_{n+1}}$）（n∈N^*）在函数y=f（x）的图象上，且a₁=1，a_n＞0．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设b_n=$\frac{{3}^{n}}{{{a}_{n}}^{2}}$，求数列{b_n}的前n项和S_n；
（Ⅲ）设c_n=a_n²•a_n+1²，数列{c_n}的前n项和为T_n，且T_n＜t²-t-$\frac{1}{2}$对任意的n∈N^*恒成立，求t的取值范围．

已知定义在实数集上的函数满足：① ；②；③当时，，则、、满足（）

A．

B．

C．

D．

数列中，对所有的正整数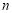都有，则（）

A． B． C． D．