题目内容
6．求不等式x2-2ax+2a-1＞0的解集．分析 由不等式x2-2ax+2a-1＞0化为（x-1）[x-（2a-1）]＞0，对a与1的大小关系分类讨论即可得出．
解答 解：由不等式x2-2ax+2a-1＞0化为（x-1）[x-（2a-1）]＞0，
由2a-1=1，解得a=1．
∴当a=1时，不等式化为（x-1）2＞0，解得x≠1，此时不等式的解集为{x|x≠1}；
当a＞1时，2a-1＞1，不等式的解集为{x|x＞2a-1，或x＜1}；
当a＜1时，2a-1＜1，不等式的解集为{x|x＞1，或x＜2a-1}．
综上可得：
当a=1时，不等式的解集为{x|x≠1}；
当a＞1时，不等式的解集为{x|x＞2a-1，或x＜1}；
当a＜1时，不等式的解集为{x|x＞1，或x＜2a-1}．
点评 本题考查了一元二次不等式的解法，考查了分类讨论方法、推理能力与计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
16．随着城市车辆的增加，城市的空气污染越来越严重，空气质量指数API一直居高不下，对人体的呼吸系统造成了严重的影响．现调查了某市500名居民的工作场所和呼吸系统健康，得到2×2列联表如下
补全2×2列联表，并回答能否有99%的把握认为“感染呼吸系统疾病和工作场所有关”．
参考公式：x2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$．
| 室外工作 | 室内工作 | 合计 | |
| 有呼吸系统疾病 | 150 | ||
| 无呼吸系统疾病 | 110 | ||
| 合计 | 200 |
| P（Χ2≥k） | 0.050 0.025 0.010 |
| k | 3.841 5.024 6.635 |
1．
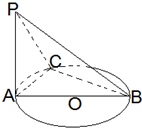如图，AB是圆O的直径，PA⊥圆O所在的平面，C是圆周上不同于A、B的任意一点，则图中互相垂直的平面共有（ ）
如图，AB是圆O的直径，PA⊥圆O所在的平面，C是圆周上不同于A、B的任意一点，则图中互相垂直的平面共有（ ）| A． | 2对 | B． | 3对 | C． | 4对 | D． | 5对 |
16．计算：$\int_1^2{{{（x-1）}^5}dx}$=（ ）
| A． | $-\frac{1}{5}$ | B． | $\frac{1}{5}$ | C． | $-\frac{1}{6}$ | D． | $\frac{1}{6}$ |