题目内容
18.已知△ABC的两个顶点A,B的坐标分别是(0,-1),(0,1),且AC,BC所在直线的斜率之积等于m(m≠0).(1)求顶点C的轨迹E的方程,并判断轨迹E为何种圆锥曲线;
(2)当m=-$\frac{1}{2}$时,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M,试问:直线OM的斜率与直线l的斜率的乘积是否为定值.若是,求出定值,若不是,请说明理由.
分析 (1)设点C(x,y),由AC,BC所在直线的斜率之积等于m(m≠0),分类讨论,即可求顶点C的轨迹E的方程,并判断轨迹E为何种圆锥曲线;
((2)当m=-$\frac{1}{2}$时,曲线E的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1(x≠0)$.设直线l:y=kx+b,(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM),联立直线方程与椭圆方程,通过韦达定理求解KOM,然后推出直线OM的斜率与l的斜率的乘积为定值.
解答 解:(1)设点C(x,y),由AC,BC所在直线的斜率之积等于m(m≠0),
得:$\frac{y-1}{x}•\frac{y+1}{x}$=m,化简得:-mx2+y2=1(x≠0).
当m<-1时,轨迹E表示焦点在y轴上的椭圆,且除去(0,1),(0,-1)两点;
当m=-1时,轨迹E表示以(0,0)为圆心,半径是1的圆,且除去(0,1),(0,-1)两点;
当-1<m<0时,轨迹E表示焦点在x轴上的椭圆,且除去(0,1),(0,-1)两点;
当m>0时,轨迹E表示焦点在y轴上的双曲线,且除去(0,1),(0,-1)两点.
(2)当m=-$\frac{1}{2}$时,曲线E的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1(x≠0)$.
设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM).
将y=kx+b代入$\frac{x^2}{8}+\frac{y^2}{4}=1$得(2k2+1)x2+4kbx+2b2-8=0
故${x_m}=\frac{{{x_1}+{x_2}}}{2}=\frac{-2kb}{{2{k^2}+1}},{y_m}=k•{x_m}+b=\frac{b}{{2{k^2}+1}}$
于是直线OM的斜率${k_{om}}=\frac{y_m}{x_m}=-\frac{1}{2k},即{k_{om}}.k=-\frac{1}{2}$
所以直线OM的斜率与直线l的斜率的乘积为定值.
点评 本题考查椭圆方程的综合应用,椭圆的方程的求法,考查分析问题解决问题的能力.

| A. | x2>6.635 | B. | x2≤6.635 | C. | x2≤3.841 | D. | x2>3.841 |
| A. | y=2x-2 | B. | y=log2x | C. | y=x2+1 | D. | y=x+1 |
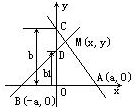 如图,二杆各绕点A(a,0)和B(-a,0)旋转,且它们在y轴上的截距的乘积bb1=a2(常数),试求旋转杆交点的轨迹方程.
如图,二杆各绕点A(a,0)和B(-a,0)旋转,且它们在y轴上的截距的乘积bb1=a2(常数),试求旋转杆交点的轨迹方程. 如图圆O是半径为1的圆,点PO、P1、P2…、P11将圆12等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3,…,11)的取值集合是{-1,-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,0,$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,1}.
如图圆O是半径为1的圆,点PO、P1、P2…、P11将圆12等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3,…,11)的取值集合是{-1,-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,0,$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,1}.