题目内容
对于非空集合A,B,定义运算:A⊕B={x|x∈A∪B,且x∉A∩B},
已知M={x|a<x<b},N={x|c<x<d},其中a,b,c,d满足a+b=c+d,ab<cd<0,则
M⊕N=( )
A.(a,d)∪(b,c) B.(c,a]∪[b,d)
C.(a,c]∪[d,b) D.(c,a)∪(d,b)
C.由题意得:a<c<0<d<b,所以M⊕N=(a,c]∪[d,b).也可以利用举特例:如a=-5,b=4,c=-3,d=2.
【误区警示】解答本题时易因搞不清a,b,c,d的关系而无法求解,错误的原因是不理解条件a+b=c+d,ab<cd<0所致.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
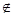 A∩B},已知两个开区间M=(a,b),N=(c,d),其中a.b.c.d满足a+b<c+d,ab=cd<0,则MN等于
A∩B},已知两个开区间M=(a,b),N=(c,d),其中a.b.c.d满足a+b<c+d,ab=cd<0,则MN等于