题目内容
15.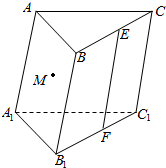 如图所示,在三棱柱ABC-A1B1C1中,E∈BC,F∈B1C1,EF∥C1C,点M∈侧面AA1B1B,设点M,E,F确定平面γ.试作出平面γ与三棱柱ABC-A1B1C1表面的交线,并说明理由.
如图所示,在三棱柱ABC-A1B1C1中,E∈BC,F∈B1C1,EF∥C1C,点M∈侧面AA1B1B,设点M,E,F确定平面γ.试作出平面γ与三棱柱ABC-A1B1C1表面的交线,并说明理由.
分析 在面ABB1A1内过M作HG∥BB1,则GE、GH、HF、EF是平面γ与三棱柱ABC-A1B1C1表面的交线.
解答  解:在面ABB1A1内过M作HG∥BB1,
解:在面ABB1A1内过M作HG∥BB1,
∵EF∥CC1,CC1∥BB1,∴HG∥EF,
∵HG?面γ,∴GE、GH、HF、EF都在平面内,
∴如图GE、GH、HF、EF是平面γ与三棱柱ABC-A1B1C1表面的交线.
点评 本题考查两相交平面交线的确定,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
7.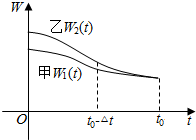 甲、乙两厂污水的排放量W与时间t的关系如图所示,治污效果较好的是( )
甲、乙两厂污水的排放量W与时间t的关系如图所示,治污效果较好的是( )
 甲、乙两厂污水的排放量W与时间t的关系如图所示,治污效果较好的是( )
甲、乙两厂污水的排放量W与时间t的关系如图所示,治污效果较好的是( )| A. | 甲 | B. | 乙 | C. | 相同 | D. | 不确定 |
4.若圆锥的高等于底面直径,则它的底面积与侧面积之比为( )
| A. | 1:2 | B. | 1:$\sqrt{3}$ | C. | 1:$\sqrt{5}$ | D. | $\sqrt{3}$:2 |
 如图,已知瞭望塔BA的高度为40m,为测得古塔DC的高度,在B处望占塔的顶部,仰角是60°,在A处再次望古塔的顶部,仰角为45°.
如图,已知瞭望塔BA的高度为40m,为测得古塔DC的高度,在B处望占塔的顶部,仰角是60°,在A处再次望古塔的顶部,仰角为45°.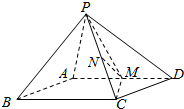 如图,四棱锥的底面ABCD是平行四边形,M是AD中点,N是PC中点.求证:MN∥平面PAB.
如图,四棱锥的底面ABCD是平行四边形,M是AD中点,N是PC中点.求证:MN∥平面PAB.