题目内容

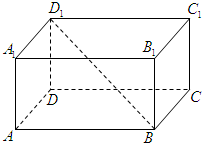已知长方体ABCD-A1B1C1D1中，AB=2，AD=AA1=1，则直线BD1与平面BCC1B1所成角的正弦值为（　　）
分析：长方体ABCD-A1B1C1D1中，由AB=2，AD=AA1=1，知BD1=
6
，再由直线BD1与平面BCC1B1所成角为∠D1BC1，由此能求出直线BD1与平面BCC1B1所成角的正弦值．
解答：解：∵长方体ABCD-A1B1C1D1中，AB=2，AD=AA1=1，
∴BD1=
4+1+1
=
6
，
∵直线BD1与平面BCC1B1所成角为∠D1BC1，
∴直线BD1与平面BCC1B1所成角的正弦值sin∠D1BC1=
D1C1
BD1
=
2
6
=
6
3
．
故选C．
点评：本题考查直线与平面所成角的正弦值的求法，解题时要认真审题，注意等价转化思想的合理运用．
练习册系列答案
相关题目
精英家教网已知长方体ABCD-A1B1C1D1中，AB=2，BC=4，AA1=4，点M是棱D1C1的中点．
（1）试用反证法证明直线AB1与BC1是异面直线；
（2）求直线AB1与平面DA1M所成的角（结果用反三角函数值表示）．
已知长方体ABCD-A1B1C1D1中，DA=DD1=1，DC=
2
，点E是B1C1的中点，点F在AB上，建立空间直角坐标系如图所示．
（1）求
AE
的坐标及长度；
（2）求点F的坐标，使直线DF与AE的夹角为90°．
已知长方体ABCD-A1B1C1D1中，M、N分别是BB1和BC的中点，AB=4，AD=2，BB1=2
15
，求异面直线B1D与MN所成角的余弦值．
精英家教网如图，已知长方体ABCD-A1B1C1D1，AB=BC=1，BB1=2，连接B1C，过B点作B1C．
的垂线交CC1于E，交B1C于F．
（I）求证：A1C⊥平面EBD；
（Ⅱ）求直线DE与平面A1B1C所成角的正弦值．
已知长方体ABCD-A1B1C1D1，下列向量的数量积一定不为0的是（　　）
精英家教网
A、
AD1
•
B1C
B、
BD1
•
AC
C、
AB
•
AD1
D、
BD1
•
BC

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网