题目内容
已知函数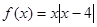
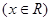 ,若存在正实数
,若存在正实数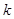 ,使得方程
,使得方程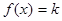 有两个根
有两个根 ,
,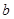 ,其中
,其中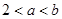 ,则
,则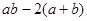 的取值范围是( )
的取值范围是( )
A.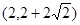 | B.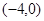 | C.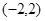 | D. |
B
解析试题分析:当x>4时,f(x)=k可化为:x²-4x-k=0,可得:b=2+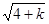 ,当x<4时,f(x)=k可化为:x²-4x+k=0可得:a=2+
,当x<4时,f(x)=k可化为:x²-4x+k=0可得:a=2+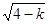 ,且0<k<4,由ab-2(a+b)= -4+
,且0<k<4,由ab-2(a+b)= -4+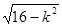 ,0<k<4,故: -4<ab-2(a+b)<0;或由f(x)=k可化为(x²-4x)²-k²=0,可得(x²-4x-k)(x²-4x+k)=0从而a=2+
,0<k<4,故: -4<ab-2(a+b)<0;或由f(x)=k可化为(x²-4x)²-k²=0,可得(x²-4x-k)(x²-4x+k)=0从而a=2+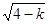 ,b=2+
,b=2+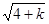 ,且0<k<4,由ab-2(a+b)= -4+
,且0<k<4,由ab-2(a+b)= -4+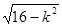 ,0<k<4故: -4<ab-2(a+b)<0.选B.
,0<k<4故: -4<ab-2(a+b)<0.选B.
考点:1.方程的根;2.不等式

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设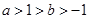 ,则下列不等式一定成立的是
,则下列不等式一定成立的是
A.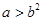 | B.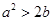 | C.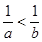 | D.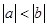 |
已知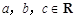 ,则下列说法正确的是 ( )
,则下列说法正确的是 ( )
A.若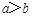 ,则 ,则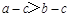 | B.若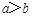 ,则 ,则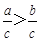 |
C.若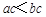 ,则 ,则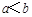 | D.若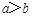 ,则 ,则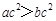 |
已知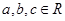 ,给出下列命题:
,给出下列命题:
①若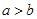 ,则
,则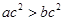 ;②若ab≠0,则
;②若ab≠0,则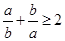 ;③若
;③若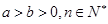 ,则
,则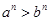 ;
;
④若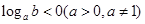 ,则a,b中至少有一个大于1.其中真命题的个数为( )
,则a,b中至少有一个大于1.其中真命题的个数为( )
| A.2 | B.3 | C.4 | D.1 |
设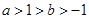 ,则下列不等式中恒成立的是 ( )
,则下列不等式中恒成立的是 ( )
A.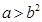 | B.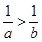 | C.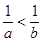 | D.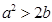 |
已知 ,则下列不等式中总成立的是( )
,则下列不等式中总成立的是( )
A.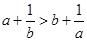 | B.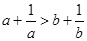 | C.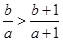 | D.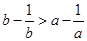 |
若a、b、c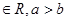 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.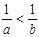 | B.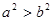 |
C.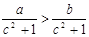 | D.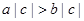 |
已知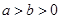 ,则下列不等式中总成立的是 ( )
,则下列不等式中总成立的是 ( )
A.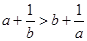 | B.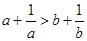 | C.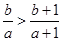 | D.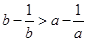 |
下列大小关系正确的是 ( )
A.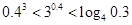 | B.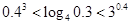 |
C. | D.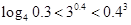 |