题目内容
1.若两个正实数x,y满足$\frac{2}{x}$+$\frac{1}{y}$=1,且x+2y>m2+2m恒成立,则实数m的取值范围是( )| A. | (-∞,-2)∪[4,+∞) | B. | (-∞,-4)∪[2,+∞) | C. | (-2,4) | D. | (-4,2) |
分析 由题意和基本不等式可得x+2y的最小值,再由恒成立可得m的不等式,解不等式可得m范围.
解答 解:∵正实数x,y满足$\frac{2}{x}$+$\frac{1}{y}$=1,
∴x+2y=(x+2y)($\frac{2}{x}$+$\frac{1}{y}$)
=4+$\frac{4y}{x}$+$\frac{x}{y}$≥4+2$\sqrt{\frac{4y}{x}•\frac{1}{y}}$=8,
当且仅当$\frac{4y}{x}$=$\frac{x}{y}$即x=4且y=2时x+2y取最小值8,
∵x+2y>m2+2m恒成立,∴8>m2+2m,
解关于m的不等式可得-4<m<2
故选:D
点评 本题考查基本不等式求最值,涉及恒成立问题和不等式的解法,属中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
12.已知a,b为不相等的两个正数,且lgab=0,则函数y=ax和y=bx的图象之间的关系是( )
| A. | 关于原点对称 | B. | 关于y轴对称 | C. | 关于x轴对称 | D. | 关于直线y=x对称 |
12.执行如图所示的程序框图,输出的结果( )


| A. | $\frac{3}{4}$ | B. | $\frac{5}{6}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{5}$ |
9.C${\;}_{6}^{1}$+C${\;}_{6}^{2}$+C${\;}_{6}^{3}$+C${\;}_{6}^{4}$+C${\;}_{6}^{5}$的值为( )
| A. | 64 | B. | 63 | C. | 62 | D. | 61 |
16.已知等差数列{an}的前n项和为Sn,若$\overrightarrow{OB}$=a1 $\overrightarrow{OA}$+a2011$\overrightarrow{OC}$,且A、B、C三点共线(O为该直线外一点),则S2011=( )
| A. | 2011 | B. | $\frac{2011}{2}$ | C. | 22011 | D. | 2-2011 |
6.设函数f(x)=-x2+2x+3,x∈[-5,5].若从区间内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
12.在△ABC中,已知$\overrightarrow{AB}•\overrightarrow{AC}$=2$\sqrt{3}$,A=60°,则△ABC的面积为( )
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
 ,且
,且 为第二象限角,则
为第二象限角,则 ( )
( ) B.
B. C.
C.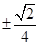 D.
D.
 中,若
中,若 ,则( )
,则( )

 或
或