题目内容
 如图,椭圆的标准方程为
如图,椭圆的标准方程为| x2 |
| a2 |
| y2 |
| b2 |
(1)求三角形PF1F2的面积.
(2)若此椭圆长轴为8,离心率为
| ||
| 2 |
分析:(1)利用直角三角形的勾股定理及椭圆的定义得到关于|PF1|,|PF2|的方程,求出|PF1|•|PF2|的值,利用直角三角形的面积公式求出△PF1F2的面积.
(2)由题知:a=4,得出椭圆的标准方程,再根据PF⊥PF2得到P为以F1F2为直径的圆上,两者结合组成方程组求解即可得点P的坐标.
(2)由题知:a=4,得出椭圆的标准方程,再根据PF⊥PF2得到P为以F1F2为直径的圆上,两者结合组成方程组求解即可得点P的坐标.
解答:解:(1)根据椭圆的定义,得|PF1|+|PF2|=2a,平方得|PF1|2+2|PF1||PF2|+|PF2|2=4a2
又PF⊥PF2∴|PF1|2+|PF2|2=4c2
∴|PF1||PF2|=2b2
∴S=
|PF1||PF2|=b2…7′.
(2)由a=4,
=
得b2=4 ….9′
∴椭圆的标准方程为
+
=1 …..10′
由PF⊥PF2∴P为以F1F2为直径的圆上.….13′
+
=1 ①x2+y2=12 ②
联列方程组 得x=±
y=±
∴点P的坐标:P1(
,
) P2(-
,
)
P3(-
,-
) P4(
,-
)….15′
又PF⊥PF2∴|PF1|2+|PF2|2=4c2
∴|PF1||PF2|=2b2
∴S=
| 1 |
| 2 |
(2)由a=4,
| c |
| a |
| ||
| 2 |
∴椭圆的标准方程为
| x2 |
| 16 |
| y2 |
| 4 |
由PF⊥PF2∴P为以F1F2为直径的圆上.….13′
| x2 |
| 16 |
| y2 |
| 4 |
联列方程组 得x=±
2
| ||
| 3 |
4
| ||
| 3 |
∴点P的坐标:P1(
2
| ||
| 3 |
4
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
P3(-
2
| ||
| 3 |
4
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
点评:本题考查椭圆的定义、椭圆的简单性质的应用,以及用待定系数法求椭圆的标准方程的方法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
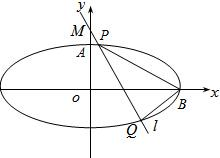 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,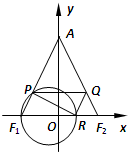 (2011•盐城模拟)(本题文科学生做)如图,在平面直角坐标系xoy中,已知F1(-4,0),F2(4,0),A(0,8),直线y=t(0<t<8)与线段AF1、AF2分别交于点P、Q.
(2011•盐城模拟)(本题文科学生做)如图,在平面直角坐标系xoy中,已知F1(-4,0),F2(4,0),A(0,8),直线y=t(0<t<8)与线段AF1、AF2分别交于点P、Q. 如图,椭圆的标准方程为
如图,椭圆的标准方程为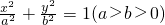 ,P为椭圆上的一点,且满足PF1⊥PF2,
,P为椭圆上的一点,且满足PF1⊥PF2, ,求点P的坐标.
,求点P的坐标. ,P为椭圆上的一点,且满足PF1⊥PF2,
,P为椭圆上的一点,且满足PF1⊥PF2,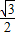 ,求点P的坐标.
,求点P的坐标.