题目内容
如图,F是中心在原点、焦点在x轴上的椭圆C的右焦点,直线l:x=4是椭圆C的右准线,F到直线l的距离等于3.
(1)求椭圆C的方程;
(2)点P是椭圆C上动点,PM⊥l,垂足为M.是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.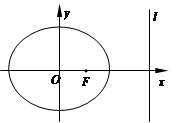
(1)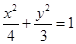 ;(2)P(
;(2)P(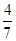 ,±
,±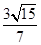 ).
).
解析试题分析:(1)求椭圆标准方程,一般利用待定系数法,利用两个独立条件确定a,b的值. 设椭圆C的方程为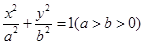 ,由已知,得
,由已知,得 ,∴
,∴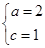 ∴b=
∴b=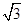 .所以椭圆C的方程为
.所以椭圆C的方程为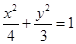 .(2)等腰三角形这个条件,是不确定的,首先需要确定腰. 由
.(2)等腰三角形这个条件,是不确定的,首先需要确定腰. 由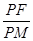 =e=
=e=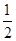 ,得PF=
,得PF=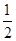 PM.∴PF≠PM.若PF=FM,则PF+FM=PM,与“三角形两边之和大于第三边”矛盾,∴PF不可能与FM相等.因此只有FM=PM,然后结合点在椭圆上条件进行列方程求解:设P(x,y)(x≠±2),则M(4,y).∴
PM.∴PF≠PM.若PF=FM,则PF+FM=PM,与“三角形两边之和大于第三边”矛盾,∴PF不可能与FM相等.因此只有FM=PM,然后结合点在椭圆上条件进行列方程求解:设P(x,y)(x≠±2),则M(4,y).∴ =4-x,
=4-x,
∴9+y2=16-8x+x2,又由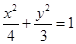 ,得y2=3-
,得y2=3-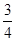 x2.∴9+3-
x2.∴9+3-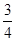 x2=16-8x+x2,∴
x2=16-8x+x2,∴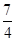 x2-8x+4=0.∴7x2-32x+16=0.∴x=
x2-8x+4=0.∴7x2-32x+16=0.∴x=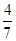 或x=4.∵x∈(-2,2),∴x=
或x=4.∵x∈(-2,2),∴x=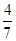 .∴P(
.∴P(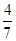 ,±
,±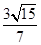 ).综上,存在点P(
).综上,存在点P(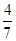 ,±
,±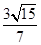 ),使得△PFM为等腰三角形.
),使得△PFM为等腰三角形.
试题解析:解:(1)设椭圆C的方程为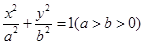
由已知,得 ,∴
,∴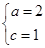 ,∴b=
,∴b=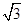 .所以椭圆C的方程为
.所以椭圆C的方程为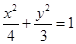
(2)由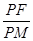 =e=
=e=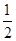 ,得PF=
,得PF=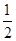 PM.∴PF≠PM.
PM.∴PF≠PM.
①若PF=FM,则PF+FM=PM,与“三角形两边之和大于第三边”矛盾,
∴PF不可能与FM 相等.
②若FM=PM,设P(x,y)(x≠±2),则M(4,y).∴ =4-x,
=4-x,
∴9+y2=16-8x+x2,又由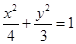 ,得y2=3-
,得y2=3-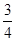 x2.∴9+3-
x2.∴9+3-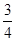 x2=16-8x+x2,
x2=16-8x+x2,
∴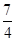 x2-8x+4=0.∴7x2-32x+16=0.∴x=
x2-8x+4=0.∴7x2-32x+16=0.∴x=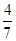 或x=4.∵x∈(-2,2),∴x=
或x=4.∵x∈(-2,2),∴x=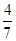 .
.
∴P(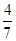 ,±
,±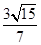 ).综上,存在点P(
).综上,存在点P(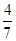 ,±
,±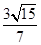 ),使得△PFM为等腰三角形.
),使得△PFM为等腰三角形.
考点:椭圆方程,椭圆第二定义

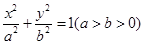 的离心率
的离心率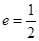 ,右焦点到直线
,右焦点到直线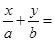 1的距离
1的距离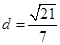 ,O为坐标原点.
,O为坐标原点.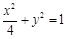 上;
上;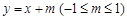 与椭圆W:
与椭圆W: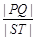 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
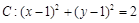 经过椭圆
经过椭圆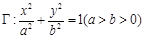 的右焦点
的右焦点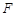 和上顶点
和上顶点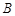 .
.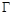 的方程;
的方程;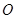 的射线
的射线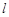 与椭圆
与椭圆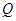 ,与圆
,与圆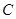 的交点为
的交点为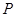 ,
,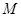 为
为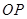 的中点,求
的中点,求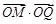 的最大值.
的最大值.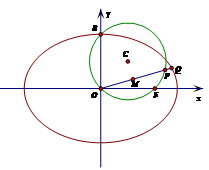
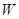 :
: 的短轴长为
的短轴长为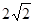 ,且斜率为
,且斜率为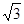 的直线
的直线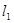 过椭圆
过椭圆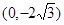 .
.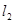 过椭圆
过椭圆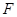 ,交椭圆于点P、Q.
,交椭圆于点P、Q.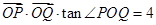 (
(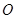 为坐标原点),求
为坐标原点),求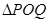 的面积;
的面积;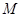 在
在 轴上,且使
轴上,且使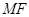 为
为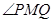 的一条角平分线,则称点
的一条角平分线,则称点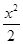 -y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.
-y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程. ,m),A点到抛物线焦点的距离为1.
,m),A点到抛物线焦点的距离为1.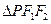 是一个以PF1为底的等腰三角形,
是一个以PF1为底的等腰三角形,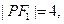 C1的离心率为
C1的离心率为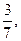 则C2的离心率
则C2的离心率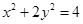 .
. ,点B在椭圆C上,且
,点B在椭圆C上,且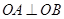 ,求线段AB长度的最小值.
,求线段AB长度的最小值.