题目内容
如图，已知边长为a的菱形ABCD中，∠ABC＝60°，PC⊥平面ABCD，E是PA的中点，求E到平面PBC的距离．
[解析] 设AC交BD于O，连结EO，则EO∥PC，
又EO⊄面PBC，PC⊂面PBC，
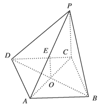
∴EO∥平面PBC，于是EO上任一点到面PBC的距离都相等，则O点到面PBC的距离即为所求．
在平面ABCD内过O作OG⊥BC于G，
∵PC⊥平面ABCD，∴PC⊥OG，
∴OG⊥面PBC.
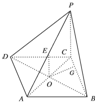
∵ABCD是菱形，∠ABC＝60°，
∴OG＝
sin∠OBC
＝×sin30°＝
a.
即E到面PBC距离为a.
练习册系列答案
轻松暑假总复习系列答案
相关题目
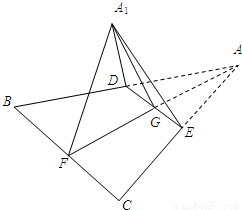
（2008•成都二模）如图，已知边长为2的正三角形ABC中线AF与中位线DE相交于点G，将此三角形沿DE折成二面角A1-DE-B，设二面角A1-DE-B的大小为θ，则当异面直线A1E与BD的夹角为60°时，cosθ的值为（ ）
—DE—B．求证：平面
⊥平面BCED．
