题目内容
如图,已知边长为2的正三角形ABC中线AF与中位线DE相交于点G,将此三角形沿DE折成二面角A1-DE-B,设二面角A1-DE-B的大小为θ,则当异面直线A1E与BD的夹角为60°时,cosθ的值为( )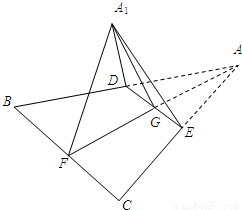
A.-

B.

C.-

D.

【答案】分析:由△ABC为等边三角形,AF为中线,知AF⊥BC.由DE为中位线,知BC∥DE,DE⊥AG,且DE⊥GF,故∠A1GF是二面角A1-DE-B的平面角,即∠A1GF=θ.由正△ABC的边长为2,知AE=BD=1, ,由异面直线A1E与BD的夹角为60°,知∠A1EF=60°,A1F=1,由
,由异面直线A1E与BD的夹角为60°,知∠A1EF=60°,A1F=1,由 能求出cosθ的值.
能求出cosθ的值.
解答:解:∵△ABC为等边三角形,AF为中线
∴AF⊥BC
又∵DE为中位线,∴BC∥DE
∴AF⊥DE
即DE⊥AG,且DE⊥GF
∵沿着DE翻折
∴DE⊥A1G
∵DE⊥AG,DE⊥GF,A1G∩AG=G
∴DE⊥平面A1GF
∴A1G⊥DE,FG⊥DE,
∴∠A1GF是二面角A1-DE-B的平面角,
即∠A1GF=θ.
∵正△ABC的边长为2,
∴AE=BD=1, ,
,
连接EF,∵AE=EC=1,BF=FC=1,
∴EF BD,
BD,
∵异面直线A1E与BD的夹角为60°,
∴∠A1EF=60°,
∴△A1EF是边长为1的等边三角形,
∴A1F=1,
∴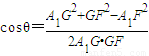
=
= .
.
故选D.
点评:本题考查二面角的余弦值的求法,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化.
 ,由异面直线A1E与BD的夹角为60°,知∠A1EF=60°,A1F=1,由
,由异面直线A1E与BD的夹角为60°,知∠A1EF=60°,A1F=1,由 能求出cosθ的值.
能求出cosθ的值.解答:解:∵△ABC为等边三角形,AF为中线
∴AF⊥BC
又∵DE为中位线,∴BC∥DE
∴AF⊥DE
即DE⊥AG,且DE⊥GF
∵沿着DE翻折
∴DE⊥A1G
∵DE⊥AG,DE⊥GF,A1G∩AG=G
∴DE⊥平面A1GF
∴A1G⊥DE,FG⊥DE,
∴∠A1GF是二面角A1-DE-B的平面角,
即∠A1GF=θ.
∵正△ABC的边长为2,
∴AE=BD=1,
 ,
,连接EF,∵AE=EC=1,BF=FC=1,
∴EF
 BD,
BD,∵异面直线A1E与BD的夹角为60°,
∴∠A1EF=60°,
∴△A1EF是边长为1的等边三角形,
∴A1F=1,
∴
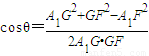
=

=
 .
.故选D.
点评:本题考查二面角的余弦值的求法,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 已知三棱锥的俯视图与侧视图如图,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图可能为( )
已知三棱锥的俯视图与侧视图如图,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图可能为( ) (2008•成都二模)如图,已知边长为2的正三角形ABC中线AF与中位线DE相交于点G,将此三角形沿DE折成二面角A1-DE-B,设二面角A1-DE-B的大小为θ,则当异面直线A1E与BD的夹角为60°时,cosθ的值为( )
(2008•成都二模)如图,已知边长为2的正三角形ABC中线AF与中位线DE相交于点G,将此三角形沿DE折成二面角A1-DE-B,设二面角A1-DE-B的大小为θ,则当异面直线A1E与BD的夹角为60°时,cosθ的值为( )




