题目内容
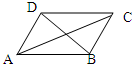 若四边形ABCD是矩形,则下列命题中不正确的是( )
若四边形ABCD是矩形,则下列命题中不正确的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据四边形ABCD是矩形再结合共线向量,相等向量,相反向量,向量的模的概念判断即可.
解答:解:∵四边形ABCD是矩形
∴AB∥CD故A,D答案对
AC=BD但
,
的方向不同故B答案错
AD=CB且AD∥CB且
,
的方向相反故C答案对
故答案选B
∴AB∥CD故A,D答案对
AC=BD但
| AC |
| BD |
AD=CB且AD∥CB且
| AD |
| CB |
故答案选B
点评:本题主要考查了平面向量的有关基本概念.解题的关键是要明白共线向量,相等向量,相反向量,向量的模的概念以及矩形的有关性质!

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知抛物线C1:x2=2y的焦点为F,以F为圆心的圆C2交C1于A,B,交C1的准线于C,D,若四边形ABCD是矩形,则圆C2的方程为( )
A、x2+(y-
| ||
B、x2+(y-
| ||
| C、x2+(y-1)2=12 | ||
| D、x2+(y-1)2=16 |
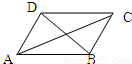
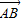 与
与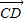 共线
共线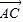 与
与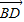 相等
相等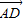 与
与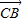 是相反向量
是相反向量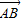 与
与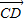 模相等
模相等