题目内容
(14分)已知数列 的前n项和为
的前n项和为 ,且满足
,且满足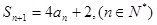 ,
,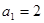 ,
,
(1)设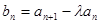 ,数列
,数列 为等比数列,求实数
为等比数列,求实数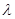 的值;
的值;
(2)设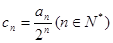 ,求数列
,求数列 的通项公式;
的通项公式;
(3)令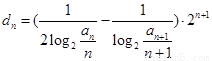 ,求数列
,求数列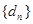 的前n项和
的前n项和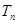 .
.
【答案】
(1)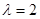 ;(2)
;(2)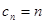 ;(3)
;(3)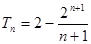
【解析】
试题分析:(1)由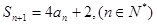 ,得
,得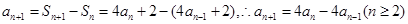 ,
,
所以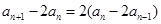 ,
,
所以数列{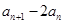 }为等比数列,又因为
}为等比数列,又因为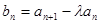 ,数列
,数列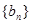 为等比数列,
为等比数列,
所以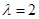 .
.
(2)由(1)知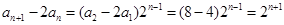
所以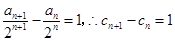 ,
,
所以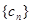 为等差数列,
为等差数列,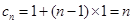 ,
,
(3) 由(2)知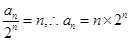 ,
,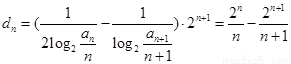 ,
,
所以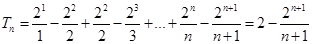 .
.
考点:等比数列的定义,等差数列的定义,数列求和.
点评:解本小题关键是利用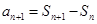 ,得到
,得到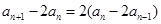 ,
,
从而得到{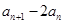 }为等比数列,因而
}为等比数列,因而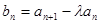 ,数列
,数列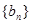 为等比数列,可确定
为等比数列,可确定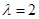 .
.
(2)再(1)的基础上,可求出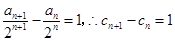 ,从而确定
,从而确定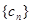 为等差数列,问题得解.
为等差数列,问题得解.
(3)求出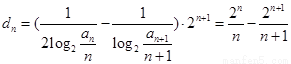 是解本小题的关键,显然再采用叠加相消求和即可.
是解本小题的关键,显然再采用叠加相消求和即可.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 求使不等式
求使不等式 的前n项和为
的前n项和为 ,
, 且满足
且满足 +n (n>1且n∈
+n (n>1且n∈ )
) ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值  的前n项和为
的前n项和为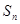 ,且
,且 ,
, ,并猜想
,并猜想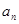 的表达式。
的表达式。