题目内容
设向量
(I)若
(II)设函数

(I)若

(II)设函数

(I)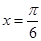 (II)
(II)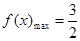
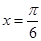 (II)
(II)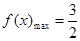
(I)由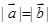 可得
可得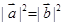 ,代入得
,代入得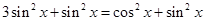
解得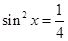 ,又
,又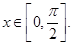 ,故,
,故,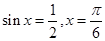
(II)由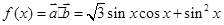 =
=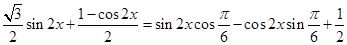
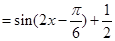 ,当
,当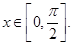 时,
时,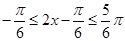 ,
,
当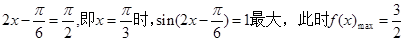
第一问直接运用模相等的关系可得关于x的方程,注意运用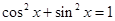 进行化简,也可用正切来运算。第二问首先运用数量积的坐标运算得到函数的解析式,然后联想二倍角公式进行化简;最后运用两角差正弦公式的逆用,从而转化为
进行化简,也可用正切来运算。第二问首先运用数量积的坐标运算得到函数的解析式,然后联想二倍角公式进行化简;最后运用两角差正弦公式的逆用,从而转化为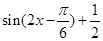 ,特别要注意
,特别要注意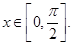 分析
分析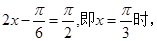
 ,学生容易忽视最值能否取到,最终得不到满分。
,学生容易忽视最值能否取到,最终得不到满分。
【考点定位】本题考查向量的坐标运算;同角三角函数基本关系;两角和差公式;二倍角公式以及三角函数的性质。
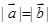 可得
可得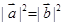 ,代入得
,代入得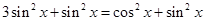
解得
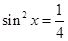 ,又
,又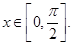 ,故,
,故,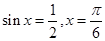
(II)由
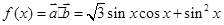 =
=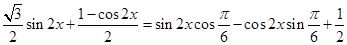
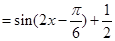 ,当
,当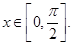 时,
时,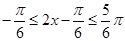 ,
,当
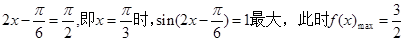
第一问直接运用模相等的关系可得关于x的方程,注意运用
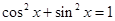 进行化简,也可用正切来运算。第二问首先运用数量积的坐标运算得到函数的解析式,然后联想二倍角公式进行化简;最后运用两角差正弦公式的逆用,从而转化为
进行化简,也可用正切来运算。第二问首先运用数量积的坐标运算得到函数的解析式,然后联想二倍角公式进行化简;最后运用两角差正弦公式的逆用,从而转化为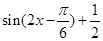 ,特别要注意
,特别要注意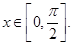 分析
分析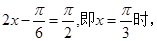
 ,学生容易忽视最值能否取到,最终得不到满分。
,学生容易忽视最值能否取到,最终得不到满分。【考点定位】本题考查向量的坐标运算;同角三角函数基本关系;两角和差公式;二倍角公式以及三角函数的性质。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
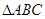 中,角
中,角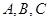 所对的边分别为
所对的边分别为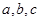 且
且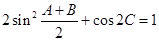 .
.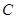 大小;
大小;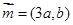 ,向量
,向量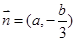 ,
,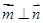 ,
,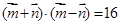 ,求
,求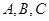 的对边分别为
的对边分别为 ,已知
,已知 ,
, .
. 和
和 ;
; ,求
,求 的面积.
的面积.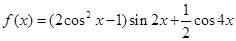
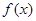 的最小正周期及最大值;
的最小正周期及最大值;
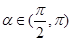 ,且
,且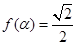 ,求
,求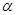 的值.
的值.

 的单调增区间;
的单调增区间;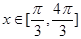 ,求
,求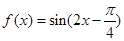 , 有如下四个命题:
, 有如下四个命题: 是函数
是函数 的一个中心对称点;
的一个中心对称点; ;
; ,且
,且 ,则
,则 (
( );
); 个单位后变为偶函数,则
个单位后变为偶函数,则 的最小值是
的最小值是 ;
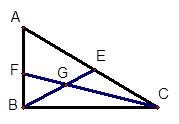
;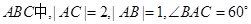 ,G是三角形
,G是三角形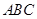 的重心,求
的重心,求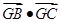 .
.
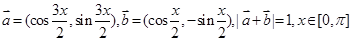 ,求x。
,求x。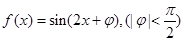 向左平移
向左平移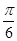 个单位后是奇函数,则函数
个单位后是奇函数,则函数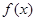 在
在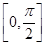 上的最小值为( )
上的最小值为( )
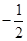


 求
求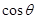 的值
的值